一台机器按不同的转速生产出来的某机械零件有一些会有缺点.每小时生产有缺点零件的多少.随机器的运转的速度而变化.下表为抽样试验的结果:转速x(转/秒-1)1614128每小时生产有缺点的零件数y(件)11985(1)画出散点图,(2)已知y对x有线性相关关系.求回归方程,(3)若实际生产中.允许每小时生产的产品中有缺点的零件最多为10个.那么机器的� 题目和参考答案——青夏教育精英家教网—

11．一台机器按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器的运转的速度而变化，下表为抽样试验的结果：

转速x（转/秒^-1）	16	14	12	8
每小时生产有缺点的零件数y（件）	11	9	8	5

（1）画出散点图；
（2）已知y对x有线性相关关系，求回归方程；
（3）若实际生产中，允许每小时生产的产品中有缺点的零件最多为10个，那么机器的运转速度应控制在什么范围内？
附：线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$．中，$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}-\stackrel{∧}{b}\overline{x}$，其中$\overline{x}$，$\overline{y}$为样本平均值．

分析（1）利用所给的数据画出散点图；
（2）先做出横标和纵标的平均数，做出利用最小二乘法求线性回归方程的系数的量，做出系数，写出线性回归方程．
（3）根据上一问做出的线性回归方程，使得函数值小于或等于10，解出不等式．

解答解：（1）散点图，如图所示．

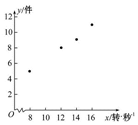
（2）由散点图可知，两变量之间具有线性相关关系．$\overline{x}$=12.5，$\overline{y}$=8.25，
$\stackrel{∧}{b}$=$\frac{438-4×12.5×8.25}{660-4×12．{5}^{2}}$≈0.7286，$\stackrel{∧}{a}$=8.25-0.7286×12.5≈-0.8571，
回归直线方程为：$\stackrel{∧}{y}$=0.7286x-0.8571；
（3）由上一问可知0.7286x-0.8571≤10，
解得x≤14.9013，所以机器的运转速度应控制在14.9转/秒内．

点评本题考查线性回归分析，考查线性回归方程，考查线性回归方程的应用，考查不等式的解法，是一个综合题目．

练习册系列答案

红色风暴初中生学业考试模拟与预测系列答案

鸿图图书寒假作业假期作业吉林大学出版社系列答案