
科目:高中数学 来源: 题型:
设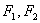 分别为双曲线
分别为双曲线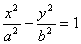
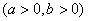 的左、右焦点,
的左、右焦点,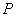 为双曲线右支上任一点。若
为双曲线右支上任一点。若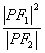 的最小值为
的最小值为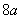 ,则该双曲线的离心率的取值范围是( )
,则该双曲线的离心率的取值范围是( )
A.(1,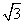 ] B.(1,3) C.(1,3] D.[
] B.(1,3) C.(1,3] D.[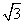 ,3)
,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线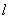 与双曲线
与双曲线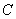 一支交于
一支交于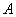 ,
,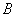 两点,
两点, 为双曲线的两个焦点,则
为双曲线的两个焦点,则 在 ( )
在 ( )
A.以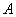 ,
,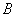 为焦点的椭圆上或线段
为焦点的椭圆上或线段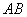 的垂直平分线上
的垂直平分线上
B.以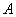 ,
,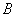 为焦点的双曲线上或线段
为焦点的双曲线上或线段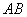 的垂直平分线上
的垂直平分线上
C.以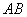 为直径的圆上或线段
为直径的圆上或线段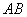 的垂直平分线上
的垂直平分线上
D.以上说法均不正确
查看答案和解析>>
科目:高中数学 来源: 题型:
下列命题正确的个数是( )
①“在三角形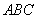 中,若
中,若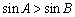 ,则
,则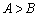 ”的逆命题是真命题;②命题
”的逆命题是真命题;②命题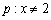 或
或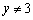 ,命题
,命题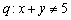 则
则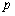 是
是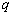 的必要不充分条件;③“
的必要不充分条件;③“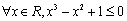 ”的否定是“
”的否定是“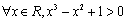 ”;④若随机变量
”;④若随机变量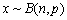 ,则
,则 ⑤回归分析中,回归方程可以是非线性方程.
⑤回归分析中,回归方程可以是非线性方程.
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数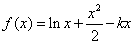 ,其中常数
,其中常数 .
.
(1) 求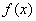 的单调增区间与单调减区间;
的单调增区间与单调减区间;
(2)若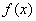 存在极值且有唯一零点
存在极值且有唯一零点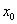 ,求
,求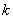 的取值范围及不超过
的取值范围及不超过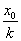 的最大整数
的最大整数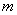 .
.
请考生在第22、23、24三题中任选一题做答,如果多做。则按所做的第一题记分.答题时用2B铅笔在答题卡上把所选的题号涂黑.
查看答案和解析>>
科目:高中数学 来源: 题型:
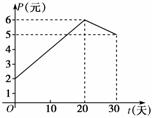
某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在下图中的两条线段上;该股票在30天内的日交易量Q(万股)与时间t(天)的部分数据如下表所示:
| 第t天 | 4 | 10 | 16 | 22 |
| Q(万股) | 36 | 30 | 24 | 18 |
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)在(2)的结论下,用y表示该股票日交易额(万元),写出y关于t的函数关系式,并求在这30天中第几天日交易额最大,最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com