
分析 (1)使用分析法证明;
(2)设0<x1<x2,利用(1)的结论和对数函数的性质化简f(x1)-f(x2)判断其符号,得出结论;
(3)由(2)的结论及f(9)=0列出不等式组,解出n即可得出M中元素的个数.
解答 (1)证明:∵x2+1>0,x2>0,
欲证:$\frac{{x}_{1}+1}{{x}_{2}+1}>\frac{{x}_{1}}{{x}_{2}}$,
只需证:x2(x1+1)>x1(x2+1),
即证:x1x2+x2>x1x2+x1,
只需证:x2>x1,
显然x2>x1成立,
∴$\frac{{x}_{1}+1}{{x}_{2}+1}>\frac{{x}_{1}}{{x}_{2}}$.
(2)解:f(x)的定义域为(0,+∞).
设0<x1<x2,则f(x1)-f(x2)=lg(x1+1)-lg(x2+1)+$\frac{1}{2}$log3x2-$\frac{1}{2}$log3x1
=lg$\frac{{x}_{1}+1}{{x}_{2}+1}$+$\frac{1}{2}$log3$\frac{{x}_{2}}{{x}_{1}}$=lg$\frac{{x}_{1}+1}{{x}_{2}+1}$-log9$\frac{{x}_{1}}{{x}_{2}}$.
∵0<x1<x2,
∴0<$\frac{{x}_{1}}{{x}_{2}}$<$\frac{{x}_{1}+1}{{x}_{2}+1}$<1,∴lg$\frac{{x}_{1}+1}{{x}_{2}+1}$>log9$\frac{{x}_{1}+1}{{x}_{2}+1}$>log9 $\frac{{x}_{1}}{{x}_{2}}$,
∴f(x1)-f(x2)=lg$\frac{{x}_{1}+1}{{x}_{2}+1}$-log9$\frac{{x}_{1}}{{x}_{2}}$>log9$\frac{{x}_{1}}{{x}_{2}}$-log9$\frac{{x}_{1}}{{x}_{2}}$=0.
∴f(x1)>f(x2),
∴f(x)在定义域(0,+∞)上是减函数.
(3)解:由(2)知f(x)是定义在(0,+∞)上的减函数,且f(9)=0,
∵f(n2-214n-1998)≥0,
∴0<n2-214n-1998≤9.
∴13447<(n-107)2≤13456.
∵115<$\sqrt{13447}$<116,$\sqrt{13456}$=116,n∈Z,
∴n-107=116或n-107=-116.
∴集合M有两个元素.
∴集合M有4个子集.
点评 本题考查了不等式的证明,对数函数的性质,函数单调性的应用,属于中档题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 100π | B. | $\frac{256}{3}$π | C. | $\frac{100}{3}$π | D. | $\frac{500}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
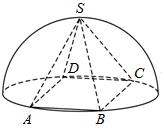 底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为$\frac{4\sqrt{2}}{3}$,则该四棱锥的外接球的体积为( )
底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为$\frac{4\sqrt{2}}{3}$,则该四棱锥的外接球的体积为( )| A. | $\frac{4\sqrt{2}}{3}$π | B. | $\frac{8\sqrt{2}}{3}$π | C. | $\frac{32\sqrt{2}}{3}$π | D. | $\frac{64\sqrt{2}}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com