
分析 作出不等式组对应的平面区域,利用z的几何意义,利用数形结合即可得到结论.
解答 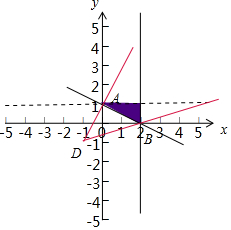 解:作出不等式组$\left\{\begin{array}{l}x≤2\\ y<1\\ x+2y-2≥0\end{array}\right.$对应的平面区域如图:
解:作出不等式组$\left\{\begin{array}{l}x≤2\\ y<1\\ x+2y-2≥0\end{array}\right.$对应的平面区域如图:
∵z=$\frac{y+1}{x+1}$,则z的几何意义为区域内的点到定点D(-1,-1)的斜率,
由图象知BD的斜率最小,AD的斜率最大,如果A在可行域则z的最大为:$\frac{1+1}{0+1}$=2,最小为:$\frac{1+0}{2+1}$=$\frac{1}{3}$,
即$\frac{1}{3}≤$z<2,
则$z=\frac{y+1}{x+1}$的取值范围是[$\frac{1}{3}$,2),
故答案为:[$\frac{1}{3}$,2).
点评 本题主要考查线性规划的应用,利用z的几何意义以及斜率的计算,通过数形结合是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美,给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”,给出下列命题:
中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美,给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”,给出下列命题:| A. | ①③ | B. | ①③④ | C. | ②③ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{\sqrt{7}}{7}$,$\frac{\sqrt{5}}{5}$]∪{$\sqrt{3}$} | B. | [$\sqrt{3}$,$\sqrt{5}$)∪{$\frac{\sqrt{7}}{7}$} | C. | [$\frac{\sqrt{7}}{7}$,$\frac{\sqrt{5}}{5}$]∪{$\sqrt{5}$} | D. | [$\sqrt{3}$,$\sqrt{7}$)∪{$\frac{\sqrt{5}}{5}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
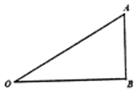 如图,某儿童公园设计一个直角三角形游乐滑梯,AO为滑道,∠OBA为直角,OB=20米,设∠AOB=θrad,一个小朋友从点A沿滑道往下滑,记小朋友下滑的时间为t秒,已知小朋友下滑的长度s与t2和sinθ的积成正比,当$θ=\frac{π}{6}$时,小朋友下滑2秒时的长度恰好为10米.
如图,某儿童公园设计一个直角三角形游乐滑梯,AO为滑道,∠OBA为直角,OB=20米,设∠AOB=θrad,一个小朋友从点A沿滑道往下滑,记小朋友下滑的时间为t秒,已知小朋友下滑的长度s与t2和sinθ的积成正比,当$θ=\frac{π}{6}$时,小朋友下滑2秒时的长度恰好为10米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com