Question

10．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{a}（2-x），x≤1}\\{2|x-5|-2，3≤x≤7}\end{array}\right.$（a＞0，a≠1）的图象上关于直线x=1对称的点有且仅有一对，则实数a的取值范围是（　　）

• A． [$\frac{\sqrt{7}}{7}$，$\frac{\sqrt{5}}{5}$]∪{$\sqrt{3}$}
• B． [$\sqrt{3}$，$\sqrt{5}$）∪{$\frac{\sqrt{7}}{7}$}
• C． [$\frac{\sqrt{7}}{7}$，$\frac{\sqrt{5}}{5}$]∪{$\sqrt{5}$}
• D． [$\sqrt{3}$，$\sqrt{7}$）∪{$\frac{\sqrt{5}}{5}$}

Answer 1

分析 若函数f（x）=$\left\{\begin{array}{l}{lo{g}_{a}（2-x），x≤1}\\{2|x-5|-2，3≤x≤7}\end{array}\right.$（a＞0，a≠1）的图象上关于直线x=1对称的点有且仅有一对，则函数y=log_ax与y=2|x-5|-2在[3，7]上有且只有一个交点，解得实数a的取值范围．

解答 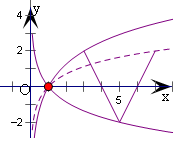解：∵函数f（x）=$\left\{\begin{array}{l}{lo{g}_{a}（2-x），x≤1}\\{2|x-5|-2，3≤x≤7}\end{array}\right.$（a＞0，a≠1）的图象上
关于直线x=1对称的点有且仅有一对，
∴函数y=log_ax，与y=2|x-5|-2在[3，7]上有且只有一个交点，
当对数函数的图象过（5，-2）点时，
由log_a5=-2，解得a=$\frac{\sqrt{5}}{5}$；
当对数函数的图象过（3，2）点时，
由log_a3=2，解得a=$\sqrt{3}$；
当对数函数的图象过（7，2）点时，
由log_a7=2，解得a=$\sqrt{7}$．
故a∈[$\sqrt{3}$，$\sqrt{7}$）∪{$\frac{\sqrt{5}}{5}$}，
故选：D．

点评 本题考查的知识点是分段函数的应用，注意运用转化思想，转化为函数的图象的交点问题，考查数形结合思想，难度中档．