已知数列{an}的前n项和Sn满足Sn+2n=2an,则数列{an}的通项公式为 .
【答案】
分析:由S
n+2n=2a
n,知S
n=2a
n-2n.当n=1 时,S
1=2a
1-2,则a
1=2,当n≥2时,S
n-1=2a
n-1-2(n-1),故a
n=2a
n-1+2,由此能够求出数列{a
n}的通项公式a
n.
解答:解:∵S
n+2n=2a
n,∴S
n=2a
n-2n,
当n∈N
*时,S
n=2a
n-2n,①
当n=1时,S
1=2a
1-2,则a
1=2,
则当n≥2,n∈N
*时,S
n-1=2a
n-1-2(n-1).②
①-②,得a
n=2a
n-2a
n-1-2,
即a
n=2a
n-1+2,
∴a
n+2=2(a
n-1+2)
∴
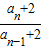
=2,
∴{a
n+2}是以a
1+2为首项,以2为公比的等比数列.
∴a
n+2=4•2
n-1,
∴a
n=2
n+1-2.
故答案为:a
n=2
n+1-2.
点评:本题考查等比数列的证明和求数列{a
n}的通项公式a
n,解题时要认真审题,注意构造法和错位相减法的合理运用.

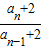 =2,
=2,
