
已知函数 (a,b均为正常数).
(a,b均为正常数).
(1)求证:函数 在
在 内至少有一个零点;
内至少有一个零点;
(2)设函数在 处有极值,
处有极值,
①对于一切 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围;
②若函数f(x)在区间 上是单调增函数,求实数
上是单调增函数,求实数 的取值范围.
的取值范围.
(1)详见解析;(Ⅱ)① ②
②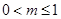 .
.
解析试题分析:(Ⅰ)证明函数 在
在 内至少有一个零点,可由零点的存在性定理考察
内至少有一个零点,可由零点的存在性定理考察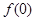 和
和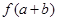 的符号,若
的符号,若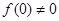 且
且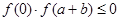 ,则结论成立,若
,则结论成立,若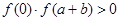 ,可将区间
,可将区间 进行适当分割,再依上面方法进行,直到找到函数的零点的存在区间;(Ⅱ)易知
进行适当分割,再依上面方法进行,直到找到函数的零点的存在区间;(Ⅱ)易知 ,从而求出
,从而求出 的值.
的值.
①不等式 恒成立可化分离参数转化为求函数在区间
恒成立可化分离参数转化为求函数在区间 上的最值问题,这是一个普通的三角函数问题,通过判断三角函数的单调性容易解决;②函数在一个已知区间上为增函数,求参数的取值范围问题,通常有两种方法,一是用在这个区间上导函数的符号确定,一般三角函数不用此方法,二是求出函数的单调递增区间,它必包含已知区间,然后考察参数的取值范围.
上的最值问题,这是一个普通的三角函数问题,通过判断三角函数的单调性容易解决;②函数在一个已知区间上为增函数,求参数的取值范围问题,通常有两种方法,一是用在这个区间上导函数的符号确定,一般三角函数不用此方法,二是求出函数的单调递增区间,它必包含已知区间,然后考察参数的取值范围.
试题解析:(1)证明: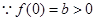 ,
,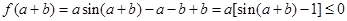

所以,函数 在
在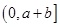 内至少有一个零点 4分
内至少有一个零点 4分
(2)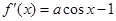 由已知得:
由已知得: 所以a=2,
所以a=2,
所以 5分
5分
①不等式 恒成立可化为:
恒成立可化为: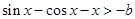
记函数

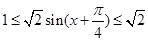 ,所以
,所以 在
在 恒成立 8分
恒成立 8分
函数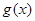 在
在 上是增函数,最小值为
上是增函数,最小值为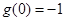
所以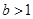 , 所以
, 所以 的取值范围是
的取值范围是 10分
10分
②由 得:
得: ,所以
,所以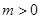 11分
11分
令 ,可得
,可得 13分
13分
∵函数 在区间(
在区间(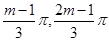 )上是单调增函数,
)上是单调增函数,
∴ 14分
14分
∴ ,
,
∵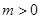 ,∴
,∴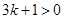 ,
,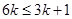 ∴
∴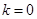 ∴
∴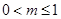 16分
16分
考点:函数的零点、三角函数的性质.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com