已知函数
.
（1）当
时，画出函数
的简图，并指出的单调递减区间；
（2）若函数有4个零点，求a的取值范围．
科目：高中数学 来源： 题型：解答题
湖南省环保研究所对长沙市中心每天环境放射性污染情况进行调查研究后，发现一天中环境综合放射性污染指数
与时刻x的关系为
，其中a是与气象有关的参数，且
，若用每天的最大值作为当天的综合放射性污染指数，并记作
.
(Ⅰ)令
，求t的取值范围；
(Ⅱ)省政府规定，每天的综合放射性污染指数不得超过2，试问目前市中心的综合放射性污染指数是否超标？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某建筑公司要在一块宽大的矩形地面（如图所示）上进行开发建设，阴影部分为一公共设施建设不能开发，且要求用栏栅隔开（栏栅要求在一直线上），公共设施边界为曲线
的一部分，栏栅与矩形区域的边界交于点
，交曲线于点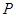
，设
．
（1）将△
（
为坐标原点）的面积
表示成
的函数
；
（2）若在
处，取得最小值，求此时
的值及的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
(a，b均为正常数).
（1）求证：函数
在
内至少有一个零点；
（2）设函数在
处有极值，
①对于一切
，不等式
恒成立，求
的取值范围；
②若函数f(x)在区间
上是单调增函数，求实数
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
和
；
.
,据此可画出图象，由图象可得
，得
,这样问题转化为曲线
与直线
有4个不同交点,由(1)题中的图像可得a的取值范围.
,
的图象分别与
轴、
轴交于
两点，且
，函数
，当
，时，求函数
的值域.
是定义在
上的增函数，且
的值；（2）、若
，解不等式
.
：
上存在零点，求实数
的取值范围；
，当
时，
的值域为区间
，且
.
的值，据此提出一个猜想，并予以证明；
的下方.
．
时，求曲线
在原点处的切线方程；
时，讨论函数
在区间
上的单调性；
对任意
成立．