
如图,在三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
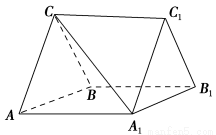
(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C=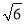 ,求三棱柱ABC-A1B1C1的体积;
,求三棱柱ABC-A1B1C1的体积;
(3)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C与平面BB1C1C所成角的正弦值.
(1)见解析(2)3(3)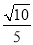
【解析】(1)如图,取AB的中点O,连接CO,A1O.
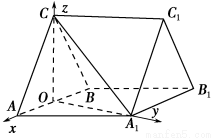
∵CA=CB,∴CO⊥AB,
又∵AA1=AB,得AA1=2AO,
又∠A1AO=60°,
∴∠AOA1=90°,即AB⊥A1O,
∴AB⊥平面A1OC,又A1C?平面A1OC,
∴AB⊥A1C.
(2)∵AB=CB=2=AC,∴CO=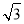 ,
,
又A1A=AB=2,∠BAA1=60°,
∴在等边三角形AA1B中,A1O=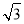 ,
,
∵A1C2=A1O2+CO2=6,
∴∠COA1=90°,即A1O⊥CO,
∴A1O⊥平面ABC,
∴VABC-A1B1C1=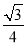 ×22×
×22×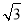 =3.
=3.
(3)作辅助线同(1)
以O为原点,OA所在直线为x轴,OA1所在直线为y轴,OC所在直线为z轴,建立如图直角坐标系,则A(1,0,0),A1(0,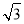 ,0),B(-1,0,0),C(0,0,
,0),B(-1,0,0),C(0,0,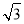 ),B1(-2,
),B1(-2,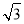 ,0),则
,0),则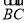 =(1,0,
=(1,0,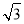 ),
),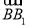 =(-1,
=(-1,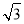 ,0),
,0),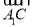 =(0,-
=(0,-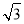 ,
,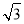 ),设n=(x,y,z)为平面BB1C1C的法向量,则
),设n=(x,y,z)为平面BB1C1C的法向量,则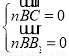 即
即 所以n=(
所以n=(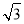 ,1,-1),
,1,-1),
则cos<n,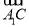 =
=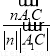 =-
=-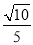 ,
,
所以A1C与平面BB1C1C所成角的正弦值为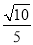 .
.


科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-3练习卷(解析版) 题型:选择题
通过随机询问110名性别不同的人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的列联表:
| 男 | 女 | 总计 |
走天桥 | 40 | 20 | 60 |
走斑马线 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由K2=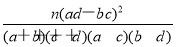 ,得K2=
,得K2= ≈7.8.
≈7.8.
附表:
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论 ( ).
A.有99%以上的把握认为“选择过马路的方式与性别有关”
B.有99%以上的把握认为“选择过马路的方式与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别无关”
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-2练习卷(解析版) 题型:填空题
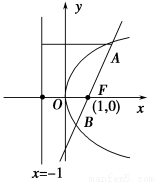
过抛物线y2=4x的焦点F的直线交该抛物线于A,B两点.若|AF|=3,
则|BF|=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-1练习卷(解析版) 题型:选择题
圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关系为( ).
A.内切 B.相交 C.外切 D.相离
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(解析版) 题型:选择题
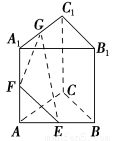
正三棱柱ABC-A1B1C1的棱长都为2,E,F,G为AB,AA1,A1C1的中点,则B1F与平面GEF所成角的正弦值为( ).
A.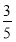 B.
B.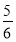 C.
C.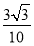 D.
D.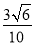
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(解析版) 题型:填空题
如图,在正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度等于________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-1练习卷(解析版) 题型:解答题
有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-4-2练习卷(解析版) 题型:选择题
若数列{an}满足 =d(n∈N*,d为常数),则称数列{an}为“调和数列”.已知正项数列
=d(n∈N*,d为常数),则称数列{an}为“调和数列”.已知正项数列 为“调和数列”,且b1+b2+…+b9=90,则b4·b6的最大值是 ( ).
为“调和数列”,且b1+b2+…+b9=90,则b4·b6的最大值是 ( ).
A.10 B.100 C.200 D.400
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-3练习卷(解析版) 题型:填空题
若曲线y=xα+1(α∈R)在点(1,2)处的切线经过坐标原点,则α=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com