
 ,求实数λ的值.
,求实数λ的值.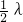 )2+
)2+ .t∈[1,4]
.t∈[1,4]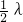 <1即λ<2时,[h(t)]max=h(1)=λ-1=
<1即λ<2时,[h(t)]max=h(1)=λ-1= ,
,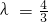 ,符合条件-------------------------
,符合条件-------------------------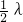 <4,即2≤λ<8时,[h(t)]max=h(
<4,即2≤λ<8时,[h(t)]max=h(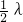 )=
)= =
=
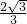 ∉[2,8),不符合题意,舍去----
∉[2,8),不符合题意,舍去----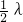 ≥4,即λ≥8时,[h(t)]max=h(4)=4λ-16=
≥4,即λ≥8时,[h(t)]max=h(4)=4λ-16=
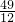 <8,不符合题意,舍去------------------
<8,不符合题意,舍去------------------ 时,实数λ的值
时,实数λ的值 .---------------------------
.---------------------------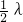 )2+
)2+ ,其中t∈[1,4].再根据二次函数的单调性进行分类讨论,分别建立关于λ的方程,解之并加以检验,最后综合可得函数g(x)的最大值是
,其中t∈[1,4].再根据二次函数的单调性进行分类讨论,分别建立关于λ的方程,解之并加以检验,最后综合可得函数g(x)的最大值是 时,实数λ的值
时,实数λ的值 .
.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com