练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．在正方体ABCD-A1B1C1D1中，O为正方形ABCD的中心，M为DD1的中点，P为棱A1B1的中点，则异面直线OP与MA所成的角为（　　）
    A．30°B．45°C．60°D．90°

    分析 正方体ABCD-A1B1C1D1中，O为正方形ABCD的中心，M为DD1的中点，P为棱A1B1的中点，与中点，找（作）中点的思想．取AD中点N，则ON⊥平面ADD1A1，A1N为OP在平面ADD1A1上的射影，在正方形ADD1A1中，DM=AN，AD=AA1，∴Rt△A1NA≌Rt△AMD，∴AM⊥A1N，从而得到AM⊥OP．

    解答 取AD中点N，则ON⊥平面ADD1A1，A1N为OP在平面ADD1A1上的射影，
    在正方形ADD1A1中，DM=AN，AD=AA1，∴Rt△A1NA≌Rt△AMD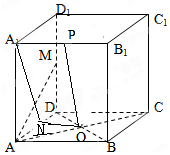
    ∴AM⊥A1N
    由三垂线定理可知AM⊥OP．
    则异面直线OP与MA所成的角为90°．
    故选D．

    点评 本题考查两条异面直线所成角的大小的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=m-|x-2|，m∈R，f（x+2）≥0的解集为[-2，2]．
    （1）求m的值；
    （2）若?x∈R，f（x）≥-|2x-1|-t2+$\frac{3}{2}$t恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

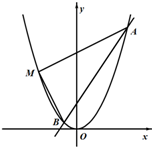    19．已知抛物线x2=2py（p＞0）上一点$P（t，\frac{7}{8}）$到抛物线焦点的距离为1，直线3x-2y+1=0与抛物线交于A，B两点．M为抛物线上的点（异于原点），且MA⊥MB．
    （Ⅰ）求p的值；
    （Ⅱ）求△MAB面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知直线（m+1）x-2my+1=0的倾斜角是45°，则m的值是（　　）
    A．-1B．0C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．直线y=x的倾斜角和斜率分别是（　　）
    A．45°，1B．135°，-1C．90°，不存在D．180°，不存在

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

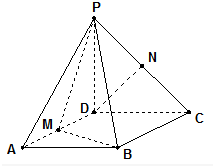    13．如图，在四棱锥P-ABCD中，底面ABCD是以∠A=60°的菱形，PD⊥底面ABCD，且PD=CD，点M，N分别为棱AD，PC的中点证明：
    （1）DN∥平面PMB；
    （2）MB⊥平面PAD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知数列{an}中，an=2an-1+n（n≥2，n∈N）．
    （1）{an}是否可能为等比数列？若可能，求出此等比数列的通项公式；若不可能，说明理由；
    （2）设bn=（-1）n（an+n+2），Sn为数列{bn}的前n项和，且对于任意的n∈N*，n≤10，都有Sn＜1，求a1的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．若a＞b＞0，则不正确的是（　　）
    A．ab＞b2B．（$\frac{1}{2}$）a＜（$\frac{1}{2}$）b
    C．log${\;}_{\frac{1}{2}}$a＞log${\;}_{\frac{1}{2}}$bD．a2＞b2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知集合U=R，A={x|-4≤x≤2}，B={x|-1＜x≤3}，则A∩B=（　　）
    A．{x|-4≤x≤2或-1＜x≤3}B．{x|-1＜x≤2}C．{x|-1≤x≤2}D．∅

    查看答案和解析>>

    同步练习册答案