
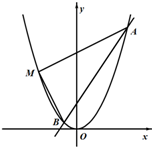
 已知抛物线x2=2py(p>0)上一点$P(t,\frac{7}{8})$到抛物线焦点的距离为1,直线3x-2y+1=0与抛物线交于A,B两点.M为抛物线上的点(异于原点),且MA⊥MB.
已知抛物线x2=2py(p>0)上一点$P(t,\frac{7}{8})$到抛物线焦点的距离为1,直线3x-2y+1=0与抛物线交于A,B两点.M为抛物线上的点(异于原点),且MA⊥MB.分析 (Ⅰ)直接由已知结合抛物线定义求得p;
(Ⅱ)由(Ⅰ)中求出的p值可得抛物线方程,联立直线与抛物线可得A,B的坐标,再结合MA⊥MB求得M的坐标,求出|AB|,由得到直线的距离公式求出M到AB的距离,代入三角形面积公式得答案.
解答 解:(Ⅰ)根据题意,$\frac{7}{8}+\frac{p}{2}=1$,即$p=\frac{1}{4}$;
(Ⅱ)由(Ⅰ)可得抛物线方程为${x}^{2}=\frac{1}{2}y$,
联立$\left\{\begin{array}{l}{3x-2y+1=0}\\{{x}^{2}=\frac{1}{2}y}\end{array}\right.$,解得A(1,2),$B(-\frac{1}{4},\frac{1}{8})$.
设点M(x0,y0),由MA⊥MB,得$\overrightarrow{MA}•\overrightarrow{MB}=0$,
即$({x_0}-1)({x_0}+\frac{1}{4})+({y_0}-2)({y_0}-\frac{1}{8})=0$,
将${y}_{0}=2{{x}_{0}}^{2}$代入上式得,$({x_0}-1)({x_0}+\frac{1}{4})+4({x_0}-1)({x_0}+1)({x_0}+\frac{1}{4})({x_0}-\frac{1}{4})=0$,
又x0≠1且${x_0}≠-\frac{1}{4}$,得$1+4({x_0}+1)({x_0}-\frac{1}{4})=0$,
解得x0=0或${x_0}=-\frac{3}{4}$,
∴点M的坐标为(0,0)(舍去)或$(-\frac{3}{4},\frac{9}{8})$.
在△MAB中,|AB|=$\sqrt{(1+\frac{1}{4})^{2}+(2-\frac{1}{8})^{2}}$=$\frac{5\sqrt{13}}{8}$.
M到直线3x-2y+1=0的距离d=$\frac{|3×(-\frac{3}{4})-2×\frac{9}{8}+1|}{\sqrt{13}}$=$\frac{7}{2\sqrt{13}}$.
∴△MAB的面积S=$\frac{1}{2}×\frac{5\sqrt{13}}{8}×\frac{7}{2\sqrt{13}}$=$\frac{35}{32}$.
点评 本题考查抛物线的简单性质,考查了直线与抛物线位置关系的应用,考查向量在求解圆锥曲线问题中的应用,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 26 | B. | 2 | C. | -2 | D. | 2或-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
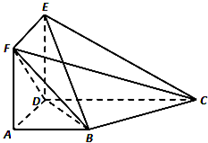 如图,多面体ABCDEF中,正方形ADEF与梯形ABCD所在平面互相垂直,已知AB∥CD,AD⊥CD,AB=2,CD=4,直线BE与平面ABCD所成的角的正切值等于$\frac{\sqrt{2}}{2}$
如图,多面体ABCDEF中,正方形ADEF与梯形ABCD所在平面互相垂直,已知AB∥CD,AD⊥CD,AB=2,CD=4,直线BE与平面ABCD所成的角的正切值等于$\frac{\sqrt{2}}{2}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -6 | C. | 11 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{1}{4}$ | D. | $-\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com