
分析 首先对f(x)进行求导,求出导函数的零点,然后分析f(x)的单调性即可求出极值.
解答 解:∵f'(x)=$\frac{1}{3}$x3-x2-8x+6;
令f'(x)=0,即x2-2x-8=0,解得x1=-2,x2=4.
当x>4,或x<-2 时,f'(x)>0,当-2<x<4 时,f'(x)<0;
∴f(x)在区间(-∞,-2),(4,+∞)上单调递增,在区间(-2,4)上单调递减;
因此,当x=-2时,f(x)有极大值,且f(-2)=$\frac{46}{3}$,
当x=4时,f(x)有极小值,且f(4)=-$\frac{62}{3}$.
点评 本题主要考查了函数的导数运算、导数与单调性以及函数的极值,属基础题.


科目:高中数学 来源: 题型:选择题
| A. | 抛一个硬币,落地后正面朝上或反面朝上 | |
| B. | 边长为a,b的长方形面积为ab | |
| C. | 从含有10%次品的100个零件中取出2个,2个都是次品 | |
| D. | 平时的百分制考试中,小强的考试成绩为105分 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $±\frac{{2\sqrt{2}}}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
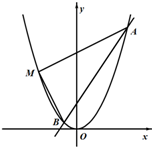 已知抛物线x2=2py(p>0)上一点$P(t,\frac{7}{8})$到抛物线焦点的距离为1,直线3x-2y+1=0与抛物线交于A,B两点.M为抛物线上的点(异于原点),且MA⊥MB.
已知抛物线x2=2py(p>0)上一点$P(t,\frac{7}{8})$到抛物线焦点的距离为1,直线3x-2y+1=0与抛物线交于A,B两点.M为抛物线上的点(异于原点),且MA⊥MB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com