
分析 (Ⅰ)利用直接法,建立方程,即可求曲线C的方程;
(Ⅱ)若满足$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,则OA⊥OB,即△AOB为等腰直角三角形,则圆心O到直线l:x-y+a=0的距离d=$\frac{\sqrt{2}}{2}$r=1.
解答 解:(Ⅰ)设点Q(x,y),依题意知$\frac{|QM|}{|QN|}$=$\frac{\sqrt{(x+2)^{2}+{y}^{2}}}{\sqrt{(x+1)^{2}+{y}^{2}}}$=$\sqrt{2}$ …(3分)
整理得x2+y2=2,∴曲线C的方程为x2+y2=2. …(6分)
(Ⅱ)若满足$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,则OA⊥OB,即△AOB为等腰直角三角形,
则圆心O到直线l:x-y+a=0的距离d=$\frac{\sqrt{2}}{2}$r=1,…(9分)
即$\frac{|a|}{\sqrt{2}}$=1,解得a=$±\sqrt{2}$.…(12分)
点评 本题考查利用直接法求轨迹方程,考查点到直线距离公式的运用,正确转化是关键.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
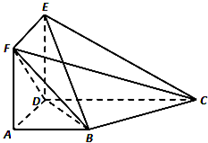 如图,多面体ABCDEF中,正方形ADEF与梯形ABCD所在平面互相垂直,已知AB∥CD,AD⊥CD,AB=2,CD=4,直线BE与平面ABCD所成的角的正切值等于$\frac{\sqrt{2}}{2}$
如图,多面体ABCDEF中,正方形ADEF与梯形ABCD所在平面互相垂直,已知AB∥CD,AD⊥CD,AB=2,CD=4,直线BE与平面ABCD所成的角的正切值等于$\frac{\sqrt{2}}{2}$查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | (-∞,-2] | C. | (-∞,-2)∪[0,2] | D. | (-∞,-2]∪[0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com