分析:(1)取BC的中点D,连AD、DF,结合F为BC1的中点,可得四边形EADF为平行四边形;即可得到EF∥AD,进而求出结论;
(2)取CC1的中点M,连EM、FM,可以先证得平面EFM∥底面ABC进而得平面EBC1与底面所成的锐二面角等于平面EBC1与平面EFM所成的锐二面角;再作MN⊥EF于N,连C1N,则EF⊥C1N,∠C1NM为平面EBC1与平面EFM所成的锐二面角的平面角,通过求其边长即可求出结论.
解答:
解:(1)取BC的中点D,连AD、DF
∵F为BC
1的中点,
∴
DF∥CC1∥AE,DF=CC1=AA1=AE,
∴四边形EADF为平行四边形.
∴EF∥AD,又AD在底面ABC上,EF不在底面ABC上
∴EF∥底面ABC.
(2)取CC
1的中点M,连EM、FM,
则EM∥AC,FM∥BC,
即平面EFM内的两条相交直线与底面ABC内的两条相交直线分别平行,
∴平面EFM∥底面ABC.
∴平面EBC
1与底面所成的锐二面角等于平面EBC
1与平面EFM所成的锐二面角.
作MN⊥EF于N,连C
1N,则EF⊥C
1N,∠C
1NM为平面EBC
1与平面EFM所成的锐二面角的平面角.
在Rt△EMF中,
EM=,MF=,
EF==,
∴
MN==.又C
1M=3,
∴在△C
1NM中,
tan∠C1NM===∴∠C
1NM=60°,
即所求锐二面角的大小为60°.
点评:本题主要考察与二面角有关的立体几何综合题.解决问题得关键在于把平面EBC1与底面所成的锐二面角转化为平面EBC1与平面EFM所成的锐二面角.

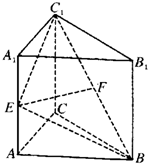 如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=
如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC= 解:(1)取BC的中点D,连AD、DF
解:(1)取BC的中点D,连AD、DF

 如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC,AA1=AC=BC=2,D、E、F分别是AB、AA1、CC1的中点,P是CD上的点.
如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC,AA1=AC=BC=2,D、E、F分别是AB、AA1、CC1的中点,P是CD上的点. 如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角.
如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角. 如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=
如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF= 如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1,AC1⊥平面A1BD,D为AC的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1,AC1⊥平面A1BD,D为AC的中点. 如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1=BC,AC1⊥平面A1BD,D为AC的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1=BC,AC1⊥平面A1BD,D为AC的中点.