练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．在数列{an}中，a1=3，nan=（1+n）an+1（n∈N*），则an．

    分析 直接由题意得到数列{nan}为常数列，结合已知条件求得an．

    解答 解：由nan=（1+n）an+1（n∈N*），得
    $\frac{（n+1）{a}_{n+1}}{n{a}_{n}}=1$，即数列{nan}为常数列．
    由a1=3，得1•a1=3．
    ∴nan=3，
    即${a}_{n}=\frac{3}{n}$．

    点评 本题考查了数列递推式，考查了等差数与等比数列的确定，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2016-2017学年河北邢台市高一上学期月考一数学试卷（解析版） 题型：解答题

    已知函数，且.

    （1）用定义法证明：函数在区间上单调递增；

    （2）若存在，使得，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．在极坐标系中，已知点P的极坐标为（4，$\frac{π}{3}$）．
    （1）若极点不变，将极轴顺时针旋转$\frac{π}{6}$，求点P在新坐标系中的极坐标；
    （2）将极点已知O′（2$\sqrt{3}$，$\frac{π}{6}$）处，极轴方向不变，求点P在新坐标系中的极坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知a＞0，b＞0．
    （I）若a+b=2，求$\frac{1}{1+a}+\frac{4}{1+b}$的最小值；
    （Ⅱ）求证：a2b2+a2+b2≥ab（a+b+1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$，右顶点为（2，0），离心率为$\frac{{\sqrt{3}}}{2}$，直线l1：y=kx+m（k≠0，m≠0）与椭圆C相交于不同的两点A，B，过AB的中点M作垂直于l1的直线l2，设l2与椭圆C相交于不同的两点C，D，且CD的中点为N．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）设原点O到直线l1的距离为d，求$\frac{{|{MN}|}}{d}$的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知x0是函数f（x）=2x+$\frac{1}{1-x}$的一个零点，若x1∈（1，x0），x2∈（x0，+∞），则$\frac{f（{x}_{2}）}{f（{x}_{1}）}$与1的大小关系为$\frac{f（{x}_{2}）}{f（{x}_{1}）}＜1$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知向量$\overrightarrow{a}$=（-1，2x），$\overrightarrow{b}$=（2，2y），且$\overrightarrow{a}$⊥$\overrightarrow{b}$，则|$\overrightarrow{a}$+$\overrightarrow{b}$|的最小值为3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

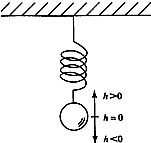    17．如图，弹簧挂着的小球上下振动，时间t（s）与小球相对于平衡位置（即静止时的位置）的高度h（cm）之间的函数关系式是h=$\sqrt{2}$sint+$\sqrt{2}$cost，t∈[0，+∞）．，则小球开始振动时h的值为$\sqrt{2}$，小球振动时最大的高度差为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．设正项等比数列{an}满足a4a6=$\frac{1}{4}$，a7=$\frac{1}{8}$，则a1的值为（　　）
    A．15B．14C．12D．8

    查看答案和解析>>

    同步练习册答案