
| A. | 在区间[$\frac{2π}{3}$,$\frac{7π}{6}$]上是增函数 | B. | 在区间[-π,-$\frac{π}{2}$]上是减函数 | ||
| C. | 在区间[-$\frac{π}{3}$,$\frac{π}{4}$]上是增函数 | D. | 在区间[$\frac{π}{3}$,$\frac{5π}{6}$]上是减函数 |
分析 根据正弦函数的性质,将图象关于x轴对称翻折,可得f(x)=|sin(x+$\frac{π}{3}$)|,即可得答案.
解答 解:由函数y=sin(x+$\frac{π}{3}$)(x∈R),可知,
当x+$\frac{π}{3}$=$-\frac{π}{2}$时,取得最小值为-1,此时x=$-\frac{5π}{6}$,
当x+$\frac{π}{3}$=0时,图象与x的交点,此时x=$-\frac{π}{3}$,
当x+$\frac{π}{3}$=$\frac{π}{2}$时,取得最大值为1,此时x=$\frac{π}{6}$,
y=sin(x+$\frac{π}{3}$)(x∈R)的图象关于x轴对称翻折,可得f(x)=|sin(x+$\frac{π}{3}$)|,
∴函数f(x)的周期为π,
∴函数f(x)的单调减区间为[$-\frac{5π}{6}+kπ$,$-\frac{π}{3}$+kπ]:单调增区间为[$-\frac{π}{3}$+kπ,$\frac{π}{6}+kπ$],k∈Z.
当k=1时,可得单调增区间为[$\frac{2π}{3}$,$\frac{7π}{6}$],
故选A.
点评 本题考查了正弦函数的性质以及图象的对称翻折问题.属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | [0,1] | C. | (-∞,-1) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 239 | B. | 240 | C. | 241 | D. | 242 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
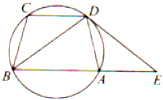 如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.
如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com