
【题目】在直角坐标系xOy中,直线C1:x=﹣2以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,C2极坐标方程为:ρ2﹣2ρcosθ﹣4ρsinθ+4=0.
(1)求C1的极坐标方程和C2的普通方程;
(2)若直线C3的极坐标方程为![]() ,设C2与C3的交点为M,N,又C1:x=﹣2与x轴交点为H,求△HMN的面积.
,设C2与C3的交点为M,N,又C1:x=﹣2与x轴交点为H,求△HMN的面积.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】2020年初,一场新冠肺炎疫情突如其来,在党中央强有力的领导下,全国各地的医务工作者迅速驰援湖北,以大无畏的精神冲在了抗击疫情的第一线,迅速控制住疫情.但国外疫情严峻,输入性病例逐渐增多,为了巩固我国的抗疫成果,保护国家和人民群众的生命安全,我国三家生物高科技公司各自组成A、B、C三个科研团队进行加急疫苗研究,其研究方向分别是灭活疫苗、核酸疫苗和全病毒疫苗,根据这三家的科技实力和组成的团队成员,专家预测这A、B、C三个团队未来六个月中研究出合格疫苗并用于临床接种的概率分别为![]() ,
,![]() ,
,![]() ,且三个团队是否研究出合格疫苗相互独立.
,且三个团队是否研究出合格疫苗相互独立.
(1)求六个月后A,B两个团队恰有一个研究出合格疫苗并用于临床接种的概率;
(2)设六个月后研究出合格疫苗并用于临床接种的团队个数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() ,
,![]() 是
是![]() 轴的正半轴上一点,
轴的正半轴上一点,![]() 交椭圆于
交椭圆于![]() ,且
,且![]() ,
,![]() 的内切圆
的内切圆![]() 半径为1.
半径为1.
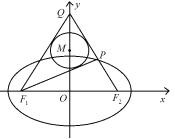
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 和圆
和圆![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某原料在市场上从2013年至2019年这7年中每年的平均价格(单位:千元/吨)数据:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
平均价格 (单位:千元/吨) |
|
|
|
|
|
|
|
(![]() 和
和![]() 线性相关性较强,求出以
线性相关性较强,求出以![]() 为解释变量
为解释变量![]() 为预报变量的线性回归方程(系数精确到
为预报变量的线性回归方程(系数精确到![]() );
);
(2)以(1)的结论为依据,预测2032年该原料价格.预估该原料价格在哪一年突破1万元/吨?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: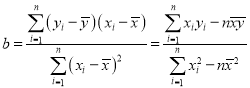 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据以往统计资料,某地车主购买甲种保险的概率为0.4,购买乙种保险但不购买甲种保险的概率为0.2.设各车主购买保险相互独立.
(1)求该地1位车主至少购买甲乙两种保险中的1种的概率;
(2)求该地3位车主中恰有1位车主甲乙两种保险都不购买的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上顶点为
,上顶点为![]() ,离心率为
,离心率为![]() , 在
, 在![]() 轴负半轴上有一点
轴负半轴上有一点![]() ,且
,且![]()
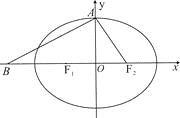
(1)若过![]() 三点的圆 恰好与直线
三点的圆 恰好与直线![]() 相切,求椭圆C的方程;
相切,求椭圆C的方程;
(2)在(1)的条件下,过右焦点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆C交于
与椭圆C交于![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出![]() 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司为客户定制了5个险种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险:戊,重大疾病保险,各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得出如下的统计图例,以下四个选项错误的是( )
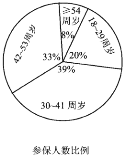
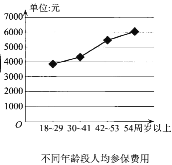
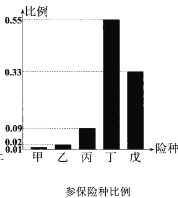
A.54周岁以上参保人数最少B.18~29周岁人群参保总费用最少
C.丁险种更受参保人青睐D.30周岁以上的人群约占参保人群的80%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足
满足![]() ,且存在常数
,且存在常数![]() ,使得对任意的
,使得对任意的![]() 都有
都有![]() ,则称数列
,则称数列![]() 为“k控数列”.
为“k控数列”.
(1)若公差为d的等差数列![]() 是“2控数列”,求d的取值范围;
是“2控数列”,求d的取值范围;
(2)已知公比为![]() 的等比数列
的等比数列![]() 的前n项和为
的前n项和为![]() ,数列
,数列![]() 与
与![]() 都是“k控数列”,求q的取值范围(用k表示).
都是“k控数列”,求q的取值范围(用k表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际上通常用年龄中位数指标作为划分国家或地区人口年龄构成的标准:年龄中位数在20岁以下为“年轻型”人口;年龄中位数在20~30岁为“成年型”人口;年龄中位数在30岁以上为“老龄型”人口.

如图反映了我国全面放开二孩政策对我国人口年龄中位数的影响.据此,对我国人口年龄构成的类型做出如下判断:①建国以来直至2000年为“成年型”人口;②从2010年至2020年为“老龄型”人口;③放开二孩政策之后我国仍为“老龄型”人口.其中正确的是( )
A.②③B.①③C.②D.①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com