已知f(x)是奇函数,g(x)是偶函数,且f(x)-g(x)=x3+x2+x.
(1)求f(x)的解析式;
(2)判断f(x)的单调性,并用定义证明.
解:(1)∵f(x)是奇函数,g(x)是偶函数,且f(x)-g(x)=x
3+x
2+x.①
∴f(-x)-g(-x)=-x
3+x
2-x,即-f(x)-g(x)=-x
3+x
2-x ②
①-②得2f(x)=2x
3+2x,∴f(x)=x
3+x
(2)函数f(x)为R上的单调增函数
证明:设x
1,x
2∈R,且x
1<x
2,
则f(x
1)-f(x
2)=x
13+x
1-(x
23+x
2)=x
13-x
23+(x
1-x
2)
=(x
1-x
2)(x
12+x
1x
2+x
22)+(x
1-x
2)=(x
1-x
2)(x
12+x
1x
2+x
22+1)
∵x
1,x
2∈R,且x
1<x
2,
∴x
1-x
2<0,x
12+x
1x
2+x
22+1=(x
1+
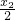
)2+
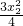
+1>0
∴(x
1-x
2)(x
12+x
1x
2+x
22+1)<0
即f(x
1)-f(x
2)<0,f(x
1)<f(x
2)
∴函数f(x)在R上为增函数.
分析:(1)将-x代入已知等式,利用函数f(x)、g(x)的奇偶性,得f(x)与g(x)的又一等式,将二者看做未知数解方程组即可得f(x)的解析式;(2)利用函数单调性的定义,设x
1,x
2∈R,且x
1<x
2,利用作差法比较f(x
1)与f(x
2)的大小,即可证明函数的单调性
点评:本题考查了函数奇偶性,解方程组法求函数的解析式,利用单调性定义证明函数单调性的方法,作差法比较大小的方法和技巧

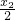 )2+
)2+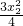 +1>0
+1>0

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案