
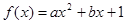 ,
,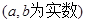 ,
,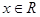 .
.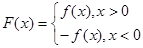
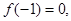 且函数
且函数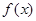 的值域为
的值域为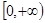 ,求
,求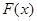 的表达式;
的表达式;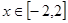 时,
时,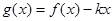 是单调函数,求实数
是单调函数,求实数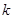 的取值范围;
的取值范围;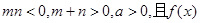 为偶函数,判断
为偶函数,判断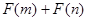 能否大于零?
能否大于零?科目:高中数学 来源:不详 题型:填空题
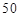 至
至 人之间,游客人数
人之间,游客人数 (人)与游客的消费总额
(人)与游客的消费总额 (元)之间近似地满足关系:
(元)之间近似地满足关系: .那么游客的人均消费额最高为_________元
.那么游客的人均消费额最高为_________元查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 立方米时,只付基本费9元和每户每月定额损耗费
立方米时,只付基本费9元和每户每月定额损耗费 元;
元; 立方米时,除了付基本费9元和定额损耗费外,超过部分每立方米付
立方米时,除了付基本费9元和定额损耗费外,超过部分每立方米付 元的超额费;
元的超额费; 不超过5元。
不超过5元。 (元)与月用水量
(元)与月用水量 (立方米)的函数关系式;
(立方米)的函数关系式;| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 4 | 17 |
| 二 | 5 | 23 |
| 三 | 2.5 | 11 |
 的值。
的值。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com