
分析 根据函数与方程的关系转化为两个函数y=tanx和y═$\frac{1}{x-π}$交点问题,利用数形结合进行求解即可.
解答 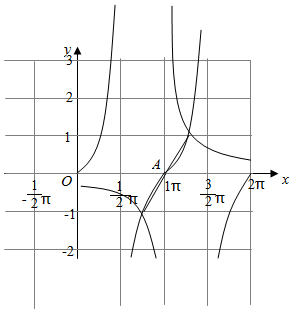 解:由f(x)=cosx+(π-x)sinx=0,
解:由f(x)=cosx+(π-x)sinx=0,
得cosx=(x-π)sinx,
当x=π时,cosπ=0不成立,则x≠π,
当cosx=0时,x=$\frac{π}{2}$或$\frac{3π}{2}$,此时,cosx=(x-π)sinx不成立,
∴cosx≠0,
即$\frac{sinx}{cosx}$=$\frac{1}{x-π}$,
即tanx═$\frac{1}{x-π}$,
分别作出函数y=tanx和y═$\frac{1}{x-π}$,在x∈[0,2π]上的图象,
则由图象知两个函数有两个交点,且关于A(π,0)对称,
设两个交点的横坐标为x1,x2,
则$\frac{{x}_{1}+{x}_{2}}{2}$=π,
则x1+x2=2π,
即函数f(x)所有的零点之和为2π,
故答案为:2π
点评 本题主要考查函数零点个数的判断和应用,利用函数与方程之间的关系转化为两个函数交点问题,以及利用数形结合是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 46 | B. | 23 | C. | 954 | D. | 317 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
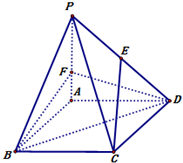 如图,四棱锥P-ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°.PA⊥面ABCD,且PA=3.F在棱PA上,且AF=1,E在棱PD上.
如图,四棱锥P-ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°.PA⊥面ABCD,且PA=3.F在棱PA上,且AF=1,E在棱PD上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
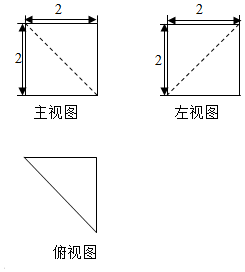 某空间几何体的三视图如图所示,则此几何体的体积是( )
某空间几何体的三视图如图所示,则此几何体的体积是( )| A. | $\frac{4}{3}$ | B. | $\frac{{4\sqrt{2}}}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{{8\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
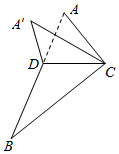 如图,已知△ABC,CD为∠ACB的角平分线,沿直线CD将△ACD翻折成△A′CD,所成二面角A′-CD-B的平面角为θ,则( )
如图,已知△ABC,CD为∠ACB的角平分线,沿直线CD将△ACD翻折成△A′CD,所成二面角A′-CD-B的平面角为θ,则( )| A. | ∠A′DB≤θ,∠A′CB≤θ | B. | ∠A′DB≤θ,∠A′CB≥θ | C. | ∠A′DB≥θ,∠A′CB≤θ | D. | ∠A′DB≥θ,∠A′CB≥θ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3,3 | B. | 3,-1 | C. | -1,3 | D. | -1,-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 6 | 2 | |
| 不肥胖 | 18 | ||
| 合计 | 30 |
| P(K2≥k) | 0.05 | 0.005 |
| k | 3.841 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com