
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 6 | 2 | |
| 不肥胖 | 18 | ||
| 合计 | 30 |
| P(K2≥k) | 0.05 | 0.005 |
| k | 3.841 | 7.879 |
分析 (1)根据列联表数据关系,可得列联表;
(2)根据列联表所给的数据,代入求观测值的公式,把观测值同临界值进行比较,得到能在犯错误的概率不超过0.5%的前提下认为肥胖与常喝碳酸饮料有关.
解答 解:(1)将列联表补充完整为
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 6 | 2 | 8 |
| 不胖 | 4 | 18 | 22 |
| 合计 | 10 | 20 | 30 |
点评 本题考查画出列联表,考查独立性检验,在求观测值时,要注意数字的代入和运算不要出错.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
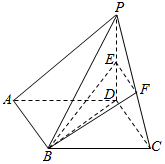 已知四棱锥P-ABCD,底面ABCD为平行四边形,PD⊥底面ABCD,AD=PD=2,DC=$\sqrt{2}$,E,F分别为PD,PC的中点,且BE与平面ABCD所成角的正切值为$\frac{{\sqrt{2}}}{2}$.
已知四棱锥P-ABCD,底面ABCD为平行四边形,PD⊥底面ABCD,AD=PD=2,DC=$\sqrt{2}$,E,F分别为PD,PC的中点,且BE与平面ABCD所成角的正切值为$\frac{{\sqrt{2}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 收入x (万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出y (万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
| A. | 11.4万元 | B. | 11.8万元 | C. | 15.2万元 | D. | 15.6万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 165 | 160 | 175 | 155 | 170 |
| y | 58 | 52 | 62 | 43 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 4 | 5 | 6 | 7 | 8 |
| y | 5 | 4 | 3 | 2 | 1 |
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②④ | C. | ①② | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一个无盖圆台形容器的上、下底面半径分别为1和2,高为$\sqrt{3}$,AD,BC是圆台的两条母线(四边形ABCD是经过轴的截面).一只蚂蚁从A处沿容器侧面(含边沿线)爬到C处,最短路程等于( )
如图,一个无盖圆台形容器的上、下底面半径分别为1和2,高为$\sqrt{3}$,AD,BC是圆台的两条母线(四边形ABCD是经过轴的截面).一只蚂蚁从A处沿容器侧面(含边沿线)爬到C处,最短路程等于( )| A. | 2$\sqrt{5}$ | B. | π+2 | C. | $\frac{π}{3}$+2$\sqrt{3}$ | D. | $\frac{4π}{3}$+2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com