
| x | 165 | 160 | 175 | 155 | 170 |
| y | 58 | 52 | 62 | 43 |
分析 先求得身高x的平均数$\overline{x}$,根据回归直线经过样本中心点$(\overline x,\overline y)$,求得$\overline{y}$,由体重y的平均数$\overline{y}$的计算公式,即可求得结果.
解答 解:由$\overline{x}$=$\frac{165+160+175+155+170}{5}$=165,
根据回归直线经过样本中心$(\overline x,\overline y)$,
可得$\overline{y}$=0.92×165-96.8=55,
由$\overline{y}$=$\frac{58+52+62+43+y}{5}$,
解得y=60,
故答案为:60.
点评 本题主要考查线性回归方程的求解与运用,解题的关键是线性回归方程 经过样本点的中心 同时注意理解线性回归方程中相关系数的意义,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
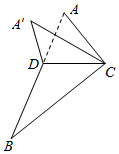 如图,已知△ABC,CD为∠ACB的角平分线,沿直线CD将△ACD翻折成△A′CD,所成二面角A′-CD-B的平面角为θ,则( )
如图,已知△ABC,CD为∠ACB的角平分线,沿直线CD将△ACD翻折成△A′CD,所成二面角A′-CD-B的平面角为θ,则( )| A. | ∠A′DB≤θ,∠A′CB≤θ | B. | ∠A′DB≤θ,∠A′CB≥θ | C. | ∠A′DB≥θ,∠A′CB≤θ | D. | ∠A′DB≥θ,∠A′CB≥θ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 上机天数x | 10 | 20 | 30 | 40 | 50 |
| 产品个数y/天 | 62 | 75 | 81 | 89 |
| A. | 67 | B. | 68 | C. | 68.3 | D. | 71 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 6 | 2 | |
| 不肥胖 | 18 | ||
| 合计 | 30 |
| P(K2≥k) | 0.05 | 0.005 |
| k | 3.841 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 气温(℃) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
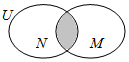 已知全集U=R,集合M={x|x2-x≤0}与集合N={x|f(x)=ln(1-|x|)}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )
已知全集U=R,集合M={x|x2-x≤0}与集合N={x|f(x)=ln(1-|x|)}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )| A. | {x|0≤x<1} | B. | {x|0<x<1} | C. | {x|0≤x≤1} | D. | {x|-1<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com