
分析 (1)分a=0与a≠0两种情况讨论函数f(x)的单调性,
(2)先求函数函数F(x)的表达式,把函数F(x)的零点转化为求方程F(x)=0的根,再构造函数,用导数研究单调性求解.
解答 解:(1)当a=0时,f(x)=2x在[1,+∞)上是单调增函数,符合题意.
当a≠0时,y=f(x)的对称轴方程为x=-$\frac{2}{a}$,
由于y=f(x)在[1,+∞)上是单调函数,所以-$\frac{2}{a}$≤1,解得a≤-2或a>0,
综上,a的取值范围是a≥0,或a≤-2.
(2)F(x)=$\frac{lnx}{x}$-(ax+2)+(2a+1),函数T(x)在区间($\frac{1}{2}$,2)内有两个不同的零点,
∴F(x)=0,即方程ax2+(1-2a)x-lnx=0在区间($\frac{1}{2}$,2)内有两个不同的实根,
设H(x)=ax2+(1-2a)x-lnx (x>0)
H′(x)=2ax+(1-2a)-$\frac{1}{x}$=$\frac{(2ax+1)(x-1)}{x}$,
令H′(x)=0,因a为正数,解得x=1或x=-$\frac{1}{2a}$(舍)
当x∈($\frac{1}{2}$,1)时,H′(x)<0,H(x)是减函数,
当x∈(1,2)时,H′(x)>0,H(x)是增函数,
为满足题意,只需H(x)在($\frac{1}{2}$,2)内有两个不相等的零点,
故$\left\{\begin{array}{l}{H(\frac{1}{2})>0}\\{{H(x)}_{min}=H(1)<0}\\{H(2)>0}\end{array}\right.$,
解得:1<a<$\frac{2+4ln2}{3}$.
点评 本题主要考查函数与导数的关系,函数的零点与方程的根之间的关系,关键是相互转化.


科目:高中数学 来源: 题型:解答题
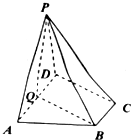 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ADC=90°,AD∥BC,平面PAD⊥底面ABCD,BC=$\frac{1}{2}$AD,PA=AD=AB=2,Q为AD的中点
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ADC=90°,AD∥BC,平面PAD⊥底面ABCD,BC=$\frac{1}{2}$AD,PA=AD=AB=2,Q为AD的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在某产品表面进行腐蚀刻度线实验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值如表:
在某产品表面进行腐蚀刻度线实验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值如表:| x(s) | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 | 70 | 90 | 120 |
| y(μm) | 6 | 10 | 10 | 13 | 16 | 17 | 19 | 23 | 25 | 29 | 46 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\widehat{y}$=x-1 | B. | $\widehat{y}$=2x+1 | C. | $\widehat{y}$=x+2 | D. | $\widehat{y}$=x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 165 | 160 | 175 | 155 | 170 |
| y | 58 | 52 | 62 | 43 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若求得相关系数r=-0.89,则y与x具备很强的线性相关关系,且为负相关 | |
| B. | 同学甲根据这组数据得到的回归模型1的残差平方和E1=1.8,同学乙根据这组数据得到的回归模型2的残差平方和E2=2.4,则模型1的拟合效果更好 | |
| C. | 用相关指数R2来刻画回归效果,模型1的相关指数R12=0.48,模型2的相关指数R22=0.91,则模型1的拟合效果更好 | |
| D. | 该回归分析只对被调查样本的总体适用 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | ab<b2 | C. | ac2<bc2 | D. | a2>ab>b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com