
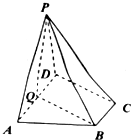
 ��ͼ��������P-ABCD�У�����ABCDΪֱ�����Σ���ADC=90�㣬AD��BC��ƽ��PAD�͵���ABCD��BC=$\frac{1}{2}$AD��PA=AD=AB=2��QΪAD���е�
��ͼ��������P-ABCD�У�����ABCDΪֱ�����Σ���ADC=90�㣬AD��BC��ƽ��PAD�͵���ABCD��BC=$\frac{1}{2}$AD��PA=AD=AB=2��QΪAD���е����� ��1���Ƶ����ı���BCDQΪƽ���ı��Σ��Ӷ�CD��BQ�����QB��AD���Ӷ�BQ��ƽ��PAD���ɴ���֤��ƽ��PQB��ƽ��PAD��
��2������CD��BQ����CD��ƽ��MBQ���Ӷ�ƽ��MBQ��Ϊƽ�����
���Ƶ���PQ��AD��PQ��ƽ��ABCD����QΪԭ�㽨���ռ�ֱ������ϵ�����������������AM��
��� ����С������13�֣�
֤������1����AD��BC��BC=$\frac{1}{2}$AD��QΪAD���е㣬
���ı���BCDQΪƽ���ı��Σ���CD��BQ��
�ߡ�ADC=90�㣬���AQB=90�� ��QB��AD��
�֡�ƽ��PAD��ƽ��ABCD����ƽ��PAD��ƽ��ABCD=AD��
��BQ��ƽ��PAD����BQ?ƽ��PQB����ƽ��PQB��ƽ��PAD�� ����4�֣�
��2������ͼ��Q��AD���е㣬����PC�ϵ�����ȡһ��M��
��ΪCD��BQ����CD?ƽ��MCD��
��CD��ƽ��MBQ����ƽ��MBQ��Ϊƽ���������7�֣�
�ڡ�PA=PD��QΪAD���е㣬��PQ��AD��
��ƽ��PAD��ƽ��ABCD����ƽ��PAD��ƽ��ABCD=AD��
��PQ��ƽ��ABCD��
��ֱ��PA��ƽ��ABCD���ɵĽ�Ϊ60�㣬
���PAQ=60�㣬��PA=2����AQ=QD=BC=1��
��ͼ����QΪԭ�㽨���ռ�ֱ������ϵ��
��ƽ��BQC�ķ�����Ϊ$\overrightarrow{n}$=��0��0��1����Q��0��0��0����P��0��0��$\sqrt{3}$����B��0��$\sqrt{3}$��0����C��-1��$\sqrt{3}$��0����
��M��x��y��z������$\overrightarrow{PM}$=��x��y��z-$\sqrt{3}$����$\overrightarrow{MC}$=��-1-x��$\sqrt{3}-y$��-z����
��$\overrightarrow{PM}=t\overrightarrow{MC}$����$\left\{\begin{array}{l}{x=t��-1-x��}\\{y=t��\sqrt{3}-y��}\\{z-\sqrt{3}=t��-z��}\end{array}\right.$�����$\left\{\begin{array}{l}{x=-\frac{t}{1+t}}\\{y=\frac{\sqrt{3}t}{1+t}}\\{z=\frac{\sqrt{3}}{1+t}}\end{array}\right.$������10�֣�
��ƽ��MBQ�У�$\overrightarrow{QB}$=��0��$\sqrt{3}$��0����$\overrightarrow{QM}$=��-$\frac{t}{1+t}$��$\frac{\sqrt{3}t}{1+t}$��$\frac{\sqrt{3}}{1+t}$����
��ƽ��MBQ������Ϊ$\overrightarrow{m}$=��$\sqrt{3}��0��t$����
�߶����M-BQ-CΪ30�㣬cos30��=$\frac{\overrightarrow{n}•\overrightarrow{m}}{|\overrightarrow{n}|•|\overrightarrow{m}|}$=$\frac{t}{\sqrt{3+0+{t}^{2}}}$=$\frac{\sqrt{3}}{2}$��
���t=3��
��A��1��0��0����M��-$\frac{3}{4}$��$\frac{3\sqrt{3}}{4}$��$\frac{\sqrt{3}}{4}$����
AM=$\sqrt{��1+\frac{3}{4}��^{2}+��0-\frac{3\sqrt{3}}{4}��^{2}+��0-\frac{\sqrt{3}}{4}��^{2}}$=$\frac{\sqrt{79}}{4}$������13�֣�
���� ���⿼�����洹ֱ��֤���������߶γ��������е��⣬����ʱҪ�������⣬ע���������ĺ������ã�


 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��B����� | B�� | ��B������� | C�� | ��B��ֱ�� | D�� | ��B�Ƕ۽� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
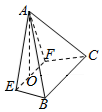 ��ͼ��������A-EFCB�У���AEFΪ�ȱ������Σ�ƽ��AEF��ƽ��EFCB��BC=4��EF=2���ı���EFCB�Ǹ�Ϊ$\sqrt{3}$�ĵ������Σ�EF��BC��OΪEF���е㣮
��ͼ��������A-EFCB�У���AEFΪ�ȱ������Σ�ƽ��AEF��ƽ��EFCB��BC=4��EF=2���ı���EFCB�Ǹ�Ϊ$\sqrt{3}$�ĵ������Σ�EF��BC��OΪEF���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��Ϊy=2x��ָ�����������Ժ���y=2x�������㣨0��1�� | |
| B�� | ��������$\frac{1}{1��2}$��$\frac{1}{2��3}$��$\frac{1}{3��4}$������ͨ�ʽΪan=$\frac{1}{n��n+1��}$��n��N*�� | |
| C�� | �ɡ�ƽ���ڴ�ֱ��ͬһֱ�ߵ���ֱ��ƽ�С�����Ƴ����ռ��д�ֱ��ͬһƽ�����ƽ��ƽ�С� | |
| D�� | ��ƽ��ֱ������ϵ��Բ�ķ���Ϊ��x-a��2+��y-b��2=r2���Ʋ�ռ�ֱ������ϵ����ķ���Ϊ��x-a��2+��y-b��2+��z-c��2=r2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
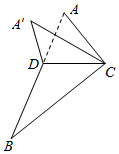 ��ͼ����֪��ABC��CDΪ��ACB�Ľ�ƽ���ߣ���ֱ��CD����ACD���۳ɡ�A��CD�����ɶ����A��-CD-B��ƽ���Ϊ�ȣ�������
��ͼ����֪��ABC��CDΪ��ACB�Ľ�ƽ���ߣ���ֱ��CD����ACD���۳ɡ�A��CD�����ɶ����A��-CD-B��ƽ���Ϊ�ȣ�������| A�� | ��A��DB�ܦȣ���A��CB�ܦ� | B�� | ��A��DB�ܦȣ���A��CB�ݦ� | C�� | ��A��DB�ݦȣ���A��CB�ܦ� | D�� | ��A��DB�ݦȣ���A��CB�ݦ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Ϊ3��ֱ������ABC-A1B1C1�У�������ֱ�������Σ�AC=2��DΪA1C1���е㣬F���߶�AA1�ϣ�$\overrightarrow{CF}•\overrightarrow{D{B}_{1}}$=0����A1F=1��
��ͼ����Ϊ3��ֱ������ABC-A1B1C1�У�������ֱ�������Σ�AC=2��DΪA1C1���е㣬F���߶�AA1�ϣ�$\overrightarrow{CF}•\overrightarrow{D{B}_{1}}$=0����A1F=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

| $\overrightarrow x$ | $\overrightarrow y$ | $\overrightarrow w$ | $\sum_{i=1}^n{{{��{x_i}-\overline x��}^2}}$ | $\sum_{i=1}^n{{{��{w_i}-\overline w��}^2}}$ | $\sum_{i=1}^n{��{x_i}-\overline x����{y_i}-\overline y��}$ | $\sum_{i=1}^n{��{w_i}-\overline w����{y_i}-\overline y��}$ |
| 46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com