

| $\overrightarrow x$ | $\overrightarrow y$ | $\overrightarrow w$ | $\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}$ | $\sum_{i=1}^n{{{({w_i}-\overline w)}^2}}$ | $\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}$ | $\sum_{i=1}^n{({w_i}-\overline w)({y_i}-\overline y)}$ |
| 46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
分析 (Ⅰ)根据散点图,即可判断出,
(Ⅱ)先建立中间量$w=\sqrt{x}$,建立y关于w的线性回归方程,根据公式求出w,问题得以解决;
(Ⅲ)(i)年宣传费x=49时,代入到回归方程,计算即可,
(ii)求出预报值得方程,根据函数的性质,即可求出.
解答 解:(Ⅰ)由散点图可以判断,$y=c+d\sqrt{x}$适合作为年销售y关于年宣传费用x的回归方程类型.…(2分)
(Ⅱ)令$w=\sqrt{x}$,先建立y关于w的线性回归方程,由于$\widehatd=\frac{{\sum_{i=1}^8{({w_i}-\overline w)({y_i}-\overline y)}}}{{\sum_{i=1}^8{{{({w_i}-\overline w)}^2}}}}$=$\frac{108.8}{16}=68$,
∴$\widehatc=\overline y-\widehatd\overline w$=563-68×6.8=100.6.
∴y关于w的线性回归方程为$\widehaty=100.6+68w$,
∴y关于x的回归方程为$\widehaty=100.6+68\sqrt{x}$.…(6分)
(Ⅲ)(ⅰ)由(Ⅱ)知,当x=49时,年销售量y的预报值$\widehaty=100.6+68\sqrt{49}$=576.6,$\widehatz=576.6×0.2-49=66.32$.…(9分)
(ⅱ)根据(Ⅱ)的结果知,年利润z的预报值$\widehatz=0.2(100.6+68\sqrt{x})-x=-x+13.6\sqrt{x}+20.12$,
∴当$\sqrt{x}$=$\frac{13.6}{2}=6.8$,即x=46.24时,$\widehatz$取得最大值.
故宣传费用为46.24千元时,年利润的预报值最大.…(12分)
点评 本题主要考查了线性回归方程和散点图的问题,准确的计算是本题的关键,属于中档题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
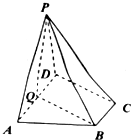 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ADC=90°,AD∥BC,平面PAD⊥底面ABCD,BC=$\frac{1}{2}$AD,PA=AD=AB=2,Q为AD的中点
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ADC=90°,AD∥BC,平面PAD⊥底面ABCD,BC=$\frac{1}{2}$AD,PA=AD=AB=2,Q为AD的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在某产品表面进行腐蚀刻度线实验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值如表:
在某产品表面进行腐蚀刻度线实验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值如表:| x(s) | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 | 70 | 90 | 120 |
| y(μm) | 6 | 10 | 10 | 13 | 16 | 17 | 19 | 23 | 25 | 29 | 46 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com