
分析 (1)当x≤0时得到f(x)=0而f(x)=2,所以无解;当x>0时解出f(x)=2求出x即可;
(2)由 t∈[1,2]时,etf(2t)+mf(t)≥0恒成立得到,得到f(t)=et-e-t,代入得到m的范围即可.
解答 解:(1)当x≤0时f(x)=0,
当x>0时,f(x)=ex-e-x,
由条件可得,ex-e-x=2,
即e2x-2×ex-1=0,解得ex=1±$\sqrt{2}$,∵ex>0,
∴ex=1+$\sqrt{2}$,
∴x=ln(1+$\sqrt{2}$).
(2)当t∈[1,2]时,etf(2t)+mf(t)≥0,
即m(e2t-1)≥-(e4t-1).∵e2t-1>0,∴m≥-(e2t+1).
∵t∈[1,2],∴-(1+e2t)∈[-1-e4,-1+e],
故m的取值范围是[e-1,+∞).
点评 本题主要考查了函数恒成立问题.属于基础题.恒成立问题多需要转化,因为只有通过转化才能使恒成立问题等到简化;转化过程中往往包含着多种数学思想的综合运用,同时转化过程更提出了等价的意识和要求.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
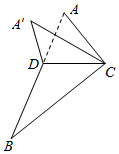 如图,已知△ABC,CD为∠ACB的角平分线,沿直线CD将△ACD翻折成△A′CD,所成二面角A′-CD-B的平面角为θ,则( )
如图,已知△ABC,CD为∠ACB的角平分线,沿直线CD将△ACD翻折成△A′CD,所成二面角A′-CD-B的平面角为θ,则( )| A. | ∠A′DB≤θ,∠A′CB≤θ | B. | ∠A′DB≤θ,∠A′CB≥θ | C. | ∠A′DB≥θ,∠A′CB≤θ | D. | ∠A′DB≥θ,∠A′CB≥θ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3,3 | B. | 3,-1 | C. | -1,3 | D. | -1,-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| $\overrightarrow x$ | $\overrightarrow y$ | $\overrightarrow w$ | $\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}$ | $\sum_{i=1}^n{{{({w_i}-\overline w)}^2}}$ | $\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}$ | $\sum_{i=1}^n{({w_i}-\overline w)({y_i}-\overline y)}$ |
| 46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 上机天数x | 10 | 20 | 30 | 40 | 50 |
| 产品个数y/天 | 62 | 75 | 81 | 89 |
| A. | 67 | B. | 68 | C. | 68.3 | D. | 71 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
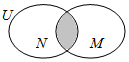 已知全集U=R,集合M={x|x2-x≤0}与集合N={x|f(x)=ln(1-|x|)}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )
已知全集U=R,集合M={x|x2-x≤0}与集合N={x|f(x)=ln(1-|x|)}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )| A. | {x|0≤x<1} | B. | {x|0<x<1} | C. | {x|0≤x≤1} | D. | {x|-1<x<1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com