
����Ŀ��
��֪��Բ![]() ���
���![]() ����ֱ��
����ֱ��![]() ���У���ԲԲ��
���У���ԲԲ��![]() �Ĺ켣��Ϊ
�Ĺ켣��Ϊ![]() ��ֱ��
��ֱ��![]() ��
��![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ������
������![]() ��б��Ϊ
��б��Ϊ![]() ��ֱ��
��ֱ��![]() ��켣
��켣![]() ��������ͬ�Ĺ�����
��������ͬ�Ĺ�����![]() ��
�� ![]() ��
�� ![]() Ϊ����ԭ��.
Ϊ����ԭ��.
��1����ԲԲ��![]() �Ĺ켣
�Ĺ켣![]() �ķ��̣�����ֱ��
�ķ��̣�����ֱ��![]() ��б��
��б��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() �ǹ켣
�ǹ켣![]() ������
������![]() ��
�� ![]() ������һ�㣬ֱ��
������һ�㣬ֱ��![]() ��
�� ![]() �ֱ����
�ֱ����![]() �Ҵ�ֱ��
�Ҵ�ֱ��![]() ���ֱ�߽���
���ֱ�߽���![]() ��
�� ![]() ��֤����
��֤���� ![]() Ϊ��ֵ��������ö�ֵ��
Ϊ��ֵ��������ö�ֵ��
��3�����ڣ�2������һ����ۣ�����![]() ��ֱ��
��ֱ��![]() �������������䣬��
�������������䣬��![]() ��ֵ������ֱ��д�������.
��ֵ������ֱ��д�������.
���𰸡���1��![]() ��2��
��2��![]()
��������������������������ߵĶ����֪Բ�ĵĹ켣Ϊ�����ߣ���������ߵķ��̣�����ֱ�ߺ������߷��̣����������ó�����![]() ��һԪ���η��̣����ø���ϵ����ϵ�ó�
��һԪ���η��̣����ø���ϵ����ϵ�ó�![]() ��
��![]() ������ֱ�������������������㣬���
������ֱ�������������������㣬���![]() �ķ�Χ��д��
�ķ�Χ��д��![]() ���̣����
���̣����![]() ���꣬��ʾ
���꣬��ʾ![]() �����������.
�����������.
���������
��1���ɶ�Բ![]() ���
���![]() ����ֱ��
����ֱ��![]() ���еã���
���еã���![]() ��
��![]() �뵽ֱ��
�뵽ֱ��![]() ������ȣ�����Բ��
������ȣ�����Բ��![]() �Ĺ켣
�Ĺ켣![]() �ķ���Ϊ��
�ķ���Ϊ�� ![]()
���� �ã�
�ã� ![]() ��
�� 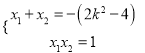
��![]() ʱ��һ�η���ֻ��һ���������Բ�����.
ʱ��һ�η���ֻ��һ���������Բ�����.
����![]() ���
���![]()
��֮��ֱ��![]() ��б��
��б��![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ![]()
��2����![]() ��
�� ![]() ��
�� ![]() ��
��
ֱ��![]() ��
�� ![]() ����
����![]() ��
�� ![]()
����![]() �Ľ���
�Ľ���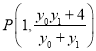 ��
��
ͬ��![]() ��
��![]() �Ľ���
�Ľ���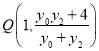
����![]()
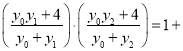
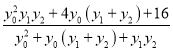
�ɣ�1���е�![]() �ã�
�ã� ![]() ������ʽ��
������ʽ��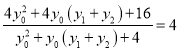
��![]()
![]()
��3����֤������Ҫ��ֻ�����۷�.
������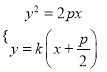 �ã�
�ã� ![]()
![]() ����
����![]() ����
����![]()
![]()
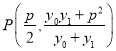 ��
�� 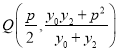
����![]()
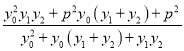
![]() ��
�� ![]()


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������A��x �� y����Բx2+y2=1��������ԭ������ʱ�뷽��������ת��12����תһ�ܣ���֪ʱ��t=0ʱ����A�������� ![]() ����0��t��12ʱ������A��������y����t����λ���룩�ĺ����ĵ������������ǣ� ��
����0��t��12ʱ������A��������y����t����λ���룩�ĺ����ĵ������������ǣ� ��
A.[0��1]
B.[1��7]
C.[7��12]
D.[0��1]��[7��12]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ѧ�������ѧ��ҵ����ʱ�䣬ijѧУͳ���˸����꼶ѧ��ÿ�������ѧ��ҵ��ƽ��ʱ�����30���ӵ�90����֮�䣬ͼ5��ͳ�ƽ����Ƶ�ʷֲ�ֱ��ͼ.

��1����ѧ������ƻ�����ҵ��ɽ�����20%��ѧ�����м��и���������ÿ�������ѧ��ҵ��ƽ��ʱ��Ϊ���ٷ������ϵ�ѧ����Ҫ�μӸ�����
��2���ִӸ����꼶ѧ������ѡ4�ˣ���4����ÿ�������ѧ��ҵ��ƽ��ʱ�䲻����50���ӵ�����Ϊ![]() ����
����![]() �ķֲ��к�����.
�ķֲ��к�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���ڵȲ�����![]() �У���֪
�У���֪![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����
����![]() ����
����![]() ȡ��ֵʱ��
ȡ��ֵʱ�� ![]() ȡ�����ֵ��������������ֵ��
ȡ�����ֵ��������������ֵ��
��2����֪����![]() ��ͨ�ʽ��
��ͨ�ʽ��![]() ��������
��������![]() ��ǰ
��ǰ![]() ���.
���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��֪����A={ x|x2��1=0 }��B={ x|ax��1=0 }��A��B=A����ʵ��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�У���ȷ���ǣ�������
A.2{x|x��2}
B.3��{x|x��2��x��1}
C.{x|x=4k��1��k��Z}��{x|x=2k+1��k��Z}
D.{x|x=3k+1��k��Z}={x|x=3k��2��k��Z}
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��x3+ax2��4��x=2��ȡ�ü�ֵ����m��n��[0��1]����f'��n��+f��m�������ֵ�ǣ� ��
A.��9
B.��1
C.1
D.��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��.
��.
(��)��![]() ������
������![]() ���ǵ�����������ʵ��
���ǵ�����������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
(��)����![]() ����
����![]() ʹ��
ʹ��![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() ��
��
��1������![]() �ĵ����������䣻
�ĵ����������䣻
��2����![]() ��
�� ![]() ����
����![]() ��
�� ![]() ��
�� ![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com