练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】知集合A={ x|x2﹣1=0 }，B={ x|ax﹣1=0 }，A∪B=A，求实数a的值．

    【答案】解：∵A={x|x2=1}={﹣1，1}，
    又∵A∪B=A得：BA，
    当a=0，ax=1无解，故B=，满足条件
    若B≠，则B={﹣1}，或Q={1}，
    即a=﹣1，或a=1
    故满足条件的实数a为：0，1，﹣1．
    【解析】知识点：并集及其运算
    解析由A∪B=A得BA，可分B=和B≠两种情况进行讨论，根据集合包含关系的判断和应用，分别求出满足条件的a值即可得到答案．
    【考点精析】解答此题的关键在于理解集合的并集运算的相关知识，掌握并集的性质：（1）AA∪B，BA∪B，A∪A=A，A∪=A,A∪B=B∪A;（2）若A∪B=B，则AB，反之也成立．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）的定义域为（﹣2，2），函数g（x）=f（x﹣1）+f（3﹣2x）．
    （1）求函数g（x）的定义域；
    （2）若f（x）是奇函数且在定义域内单调递减，求不等式g（x）≤0的解集

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数．他们研究过如图所示的三角形数：
    将三角形数1，3，6，10，…记为数列{an}，将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn}，可以推测：
    （1）b5=；
    （2）b2n﹣1= ．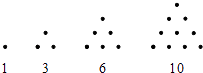

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，.

    （1）令，求的单调区间；

    （2）已知在处取得极大值，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的最小正周期为.

    (1)求的单调递增区间；

    (2)在中，角的对边分别是满足，求函数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    已知动圆恒过且与直线相切，动圆圆心的轨迹记为；直线与轴的交点为，过点且斜率为的直线与轨迹有两个不同的公共点， ， 为坐标原点.

    （1）求动圆圆心的轨迹的方程，并求直线的斜率的取值范围；

    （2）点是轨迹上异于， 的任意一点，直线， 分别与过且垂直于轴的直线交于， ，证明： 为定值，并求出该定值；

    （3）对于（2）给出一般结论：若点，直线，其它条件不变，求的值（可以直接写出结果）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义集合A={x|2x≥1}，B={y|y= }，则A∩RB=（ ）
    A.（1，+∞）
    B.[0，1]
    C.[0，1）
    D.[1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知g（x）=sin2x，将g（x）的图象向左平移 个单位长度，再将图象上各点的横坐标缩短到原来的 ，得到函数f（x）的图象，则（ ）
    A.
    B. ??
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】抽样调查某大型机器设备使用年限x和该年支出维修费用y（万元），得到数据如表

    使用年限x

    2

    3

    4

    5

    6

    维修费用y

    2.2

    3.8

    5.5

    6.5

    7.0

    部分数据分析如下 =25， yi=112.3， =90
    参考公式：线性回归直线方程为 ，
    （1）求线性回归方程；
    （2）由（1）中结论预测第10年所支出的维修费用．

    查看答案和解析>>

    同步练习册答案