
分析:利用导数研究函数y=f(x)的单调性,可得f(x)=

x-cosx在(-

,
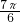
)上是增函数,结合f(

)=

得到在(-

,
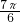
)上有且只有一个实数x=

满足f(x)=

.再由cosx的有界性和不等式的性质,证出当x≤-

时,有f(x)
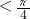
,且x≥
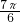
时,f(x)>

.因此当x∉(-

,
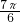
)时,方程f(x)=

没有实数根,由此即可得到方程f(x)=

只有一实数根x=

,得到本题答案.
解答:∵f(x)=

x-cosx,∴f'(x)=

+sinx,
当x∈(-

,
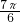
)时,因为sinx
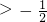
,所以f'(x)=

+sinx>0
∴f(x)=

x-cosx在(-

,
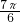
)上是增函数
∵f(

)=

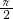
-cos

=

∴在区间(-

,
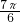
)上有且只有一个实数x=

满足f(x)=

.
又∵当x≤-

时,

x<-
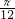
,-cosx≤1,∴当x≤-

时,f(x)=

x-cosx≤1-
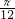
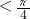
,
由此可得:当x≤-

时,方程f(x)=

没有实数根
同理可证:当x≥
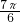
时,方程f(x)≥
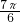
-1>

,所以方程f(x)=

也没有实数根
综上所述,方程f(x)=

只有一个实数根x=

,因此方程f(x)=

所有根的和为

故答案为:

点评:本题给出基本初等函数f(x)=

x-cosx,求方程f(x)=

所有根的和.着重考查了利用导数研究函数的单调性、函数的图象与性质、函数的零点和不等式的性质等知识,属于中档题.

 x-cosx则方程f(x)=
x-cosx则方程f(x)= 所有根的和为________.
所有根的和为________.
 x-cosx在(-
x-cosx在(- ,
,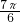 )上是增函数,结合f(
)上是增函数,结合f( )=
)= 得到在(-
得到在(- ,
,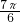 )上有且只有一个实数x=
)上有且只有一个实数x= 满足f(x)=
满足f(x)= .再由cosx的有界性和不等式的性质,证出当x≤-
.再由cosx的有界性和不等式的性质,证出当x≤- 时,有f(x)
时,有f(x)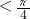 ,且x≥
,且x≥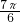 时,f(x)>
时,f(x)> .因此当x∉(-
.因此当x∉(- ,
,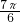 )时,方程f(x)=
)时,方程f(x)= 没有实数根,由此即可得到方程f(x)=
没有实数根,由此即可得到方程f(x)= 只有一实数根x=
只有一实数根x= ,得到本题答案.
,得到本题答案. x-cosx,∴f'(x)=
x-cosx,∴f'(x)= +sinx,
+sinx, ,
,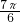 )时,因为sinx
)时,因为sinx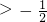 ,所以f'(x)=
,所以f'(x)= +sinx>0
+sinx>0 x-cosx在(-
x-cosx在(- ,
,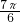 )上是增函数
)上是增函数 )=
)=
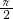 -cos
-cos =
=
 ,
,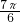 )上有且只有一个实数x=
)上有且只有一个实数x= 满足f(x)=
满足f(x)= .
. 时,
时, x<-
x<-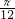 ,-cosx≤1,∴当x≤-
,-cosx≤1,∴当x≤- 时,f(x)=
时,f(x)= x-cosx≤1-
x-cosx≤1-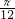
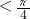 ,
, 时,方程f(x)=
时,方程f(x)= 没有实数根
没有实数根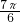 时,方程f(x)≥
时,方程f(x)≥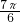 -1>
-1> ,所以方程f(x)=
,所以方程f(x)= 也没有实数根
也没有实数根 只有一个实数根x=
只有一个实数根x= ,因此方程f(x)=
,因此方程f(x)= 所有根的和为
所有根的和为

 x-cosx,求方程f(x)=
x-cosx,求方程f(x)= 所有根的和.着重考查了利用导数研究函数的单调性、函数的图象与性质、函数的零点和不等式的性质等知识,属于中档题.
所有根的和.着重考查了利用导数研究函数的单调性、函数的图象与性质、函数的零点和不等式的性质等知识,属于中档题. 

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<