
设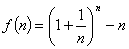 ,其中
,其中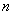 为正整数.
为正整数.
(1)求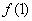 ,
,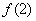 ,
,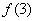 的值;
的值;
(2)猜想满足不等式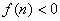 的正整数
的正整数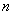 的范围,并用数学归纳法证明你的猜想.
的范围,并用数学归纳法证明你的猜想.
(1)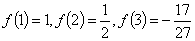 ;(2)
;(2)
【解析】
试题分析:(1)数学归纳法是一种重要的数学思想方法,主要用于解决与正整数有关的数学问题;(2)用数学归纳法证明等式问题,要“先看项”,弄清等式两边的构成规律,等式两边各有多少项,初始值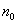 是多少;(3)由
是多少;(3)由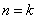 时等式成立,推出
时等式成立,推出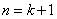 时等式成立,一要找出等式两边的变化(差异),明确变形目标;二要充分利用归纳假设,进行合理变形,正确写出证明过程,由于“猜想”是“证明”的前提和“对象”,务必保证猜想的正确性,同时必须严格按照数学归纳法的步骤书写.
时等式成立,一要找出等式两边的变化(差异),明确变形目标;二要充分利用归纳假设,进行合理变形,正确写出证明过程,由于“猜想”是“证明”的前提和“对象”,务必保证猜想的正确性,同时必须严格按照数学归纳法的步骤书写.
试题解析:解:(1)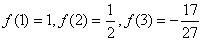 3分
3分
(2)猜想: 4分
4分
证明:①当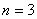 时,
时,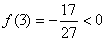 成立 5分
成立 5分
②假设当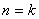
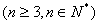 时猜想正确,即
时猜想正确,即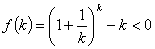
∴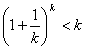
由于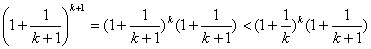
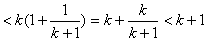 8分
8分
∴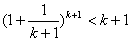 ,即
,即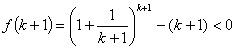 成立
成立
由①②可知,对 成立 10分
成立 10分
考点:数学归纳法及其应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
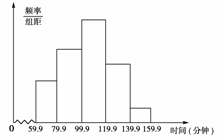
今年5月海淀区教育网开通了网上教学,某校高一年级(8)班班主任为了了解学生上网学习时间,对本班40名学生某天上网学习时间进行了调查,将数据(取整数)整理后,绘制出如图所示频率分布直方图,已知从左到右各个小组的频率分别是0.15,0.25,0.35,0.20,0.05,则根据直方图所提供的信息,这一天上网学习时间在100~119分钟之间的学生人数是________人,如果只用这40名学生这一天上网学习时间作为样本去推断该校高一年级全体学生该天的上网学习时间,这样推断是否合理?________(填“合理”或“不合理”)
查看答案和解析>>
科目:高中数学 来源: 题型:
若曲线f(x,y)=0上两个不同点处的切线重合,则称这条切线为曲线f(x,y)=0的“自公切线”.下列方程:①x2-y2=1;②y=x2-|x|;③y=3sin x+4cos x;④|x|+1=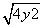 对应的曲线中存在“自公切线”的有 ( )
对应的曲线中存在“自公切线”的有 ( )
A.①② B.②③ C.①④ D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
下列有关命题的说法正确的是 ( )
A.命题“若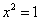 ,则
,则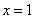 ”的否命题为:“若
”的否命题为:“若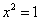 ,则
,则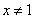 ”.
”.
B.“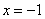 ” 是“
” 是“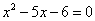 ”的必要不充分条件.
”的必要不充分条件.
C.命题“若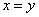 ,则
,则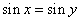 ”的逆否命题为真命题.
”的逆否命题为真命题.
D.命题“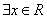 使得
使得 ”的否定是:“
”的否定是:“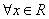 均有
均有 ”.
”.
查看答案和解析>>
科目:高中数学 来源: 题型:
解释下列概率的含义:
(1)某厂生产的电子产品合格的概率为0.997;
(2)某商场进行促销活动,购买商品满200元,即可参加抽奖活动,中奖的概率为0.6;
(3)一位气象学工作者说,明天下雨的概率是0.8;
(4)按照法国著名数学家拉普拉斯的研究结果,一个婴儿将是女孩的概率是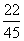 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com