Question

18．执行下面的程序框图，如果输入的N=4，那么输出的S=（　　）

• A． 1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$
• B． 1+$\frac{1}{2}$+$\frac{1}{3×2}$+$\frac{1}{4×3×2}$
• C． 1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$+$\frac{1}{5}$
• D． 1+$\frac{1}{2}$+$\frac{1}{3×2}$+$\frac{1}{4×3×2}$+

Answer 1

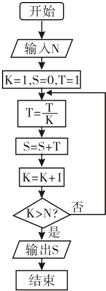
分析 根据框图的流程模拟运行程序，直到满足条件K＞4，跳出循环，计算输出S的值即可．

解答 解：由程序框图知：输入N=4时，第一次循环T=1，S=1，K=2；
第二次循环T=$\frac{1}{2}$，S=1+$\frac{1}{2}$，K=3；
第三次循环T=$\frac{1}{2×3}$，S=1+$\frac{1}{2}$+$\frac{1}{2×3}$，K=4；
第四次循环T=$\frac{1}{2×3×4}$，S=1+$\frac{1}{2}$+$\frac{1}{2×3}$+$\frac{1}{2×3×4}$，K=5；
满足条件K＞4，跳出循环，输出S=1+$\frac{1}{2}$+$\frac{1}{2×3}$+$\frac{1}{2×3×4}$．
故选：B．

点评 本题考查了直到型循环结构的程序框图，根据框图的流程模拟运行程序是解答此类问题的常用方法，属于基础题．