
| 广告费用x(万元) | 4 | 2 | 3 | 5 |
| 销售额y(万元) | 49 | 26 | 39 | 54 |
| A. | 63.6 万元 | B. | 65.5 万元 | C. | 67.7 万元 | D. | 72.0 万元 |
分析 根据表中所给的数据,广告费用x与销售额y(万元)的平均数,得到样本中心点,代入样本中心点求出a的值,写出线性回归方程.将x=6代入回归直线方程,得y,可以预报广告费用为6万元时销售额.
解答 解:由表中数据得:$\overline{x}$=3.5,$\overline{y}$=42,
又回归方程 y=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$ 中的$\stackrel{∧}{b}$为 9.4,
故a=42-9.4×3.5=9.1,
∴y=9.4x+9.1.
将x=6代入回归直线方程,得y=9.4×6+9.1=65.5(万元).
∴此模型预报广告费用为6万元时销售额为65.5(万元).
故选B.
点评 本题考查线性回归方程的求法和应用,解题的关键是正确应用最小二乘法求出线性回归方程的系数的运算,是一个中档题目.


科目:高中数学 来源: 题型:解答题
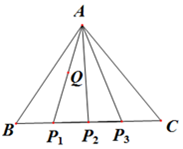 设△ABC是边长为1的正三角形,点P1,P2,P3四等分线段BC(如图所示).
设△ABC是边长为1的正三角形,点P1,P2,P3四等分线段BC(如图所示).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{18}{5}$ | B. | $\frac{14}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{9}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\root{n}{{a}^{n}}$=a | B. | $\root{6}{{y}^{2}}$=y${\;}^{\frac{1}{3}}$ | C. | a${\;}^{-\frac{3}{5}}$=$\frac{1}{\root{5}{{a}^{3}}}$ | D. | x${\;}^{-\frac{1}{3}}$=-$\root{3}{x}$(x≠0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3 个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com