
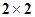 的列联表;
的列联表;
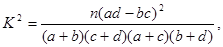 其中
其中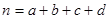 为样本容量。
为样本容量。| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:高中数学 来源:不详 题型:解答题

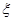 表示抽到“幸福”的人数,求
表示抽到“幸福”的人数,求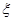 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 场次 | 投篮次数 | 命中次数 | 场次 | 投篮次数 | 命中次数 |
| 主场1 | 22 | 12 | 客场1 | 18 | 8 |
| 主场2 | 15 | 12 | 客场2 | 13 | 12 |
| 主场3 | 12 | 8 | 客场3 | 21 | 7 |
| 主场4 | 23 | 8 | 客场4 | 18 | 15 |
| 主场5 | 24 | 20 | 客场5 | 25 | 12 |
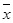 为表中10个命中次数的平均数,从上述比赛中随机选择一场,记
为表中10个命中次数的平均数,从上述比赛中随机选择一场,记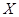 为李明在这场比赛中的命中次数,比较
为李明在这场比赛中的命中次数,比较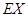 与
与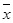 的大小(只需写出结论)
的大小(只需写出结论)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
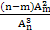 的是( )
的是( )| A.P(ξ=3) | B.P(ξ≥2) |
| C.P(ξ≤3) | D.P(ξ=2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com