Question

1．已知x，y满足$\left\{\begin{array}{l}2x+y+4≤0\\{（x+2）^2}+{（y+1）^2}≤1\end{array}\right.$，则x²+y²的取值范围是[$\frac{16}{5}$，6+2$\sqrt{5}$]．

Answer 1

分析 首先画出x，y满足的平面区域，结合x²+y²的几何意义求范围．

解答 解：由题意，x，y满足的平面区域如图阴影部分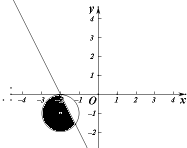，则在阴影部分（包括边界）的点中到原点距离，
最小值为原点到直线的距离为：$\frac{4}{\sqrt{5}}=\frac{4\sqrt{5}}{5}$；
最大值为$\sqrt{（-2）^{2}+（-1）^{2}}+1$=1+$\sqrt{5}$，
所以x²+y²的取值范围是[$\frac{16}{5}$，6+2$\sqrt{5}$]．
故答案为：[$\frac{16}{5}$，6+2$\sqrt{5}$]．

点评 本题考查了线性规划的运用求两个变量的代数式的值的范围；关键正确画出不等式组表示的平面区域，利用x²+y²的几何意义求最值．