解:(Ⅰ)当b=2时,f(x)=x(x-a)(x-2)=x
3-(a+2)x
2+2ax.f′(x)=3x
2-2(a+2)x+2a.…(1分)
∵△=4(a+2)
2-24a=4(a
2-2a+4)=4(a-1)
2+12>0,
∴方程f'(x)=0有两个不等的实数根x
1,x
2.…(3分)
不妨设x
1<x
2,则 f′(x)=3(x-x
1)(x-x
2).
当x<x
1时,f′(x)>0;当x
1<x<x
2时,f'(x)<0;当x>x
2时,f'(x)>0.
∴x
1是f(x)的极大值点,x
2是f(x)的极小值点.…(4分)
并且,
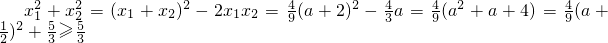
.
因此,函数f(x)有两个不同的极值点x
1,x
2,并且
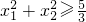
(当且仅当

时取等号)…(7分)
(Ⅱ)当a=b(a≠0)时,f(x)=x(x-a)
2=x
3-2ax
2+ax.
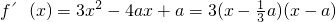
…(8分)
1若a>02,则f(x)3在
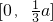
4上增函数,在
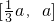
5上为减函数,在[a,a+1]6上为增函数.f(x)在[0,a+1]上的最大值为
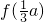
与f(a+1)中的较大者.
而

,f(a+1)=a+1.
由f(x)<2a
2在[0,a+1]上恒成立,得
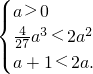
…(9分)
即
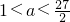
.…(11分)
②若a<0,则f(x)在[0,1-a]上为增函数.f(x)在[0,1-a]上的最大值为f(1-a)=(1-a)(1-2a)
2.
∵a<0,∴1-a>1,(1-2a)
2>(-2a)
2=4a
2>2a
2.
∴f(1-a)>2a
2.
因此,a<0不可能.…(13分)
综上所述,a的取值范围是
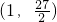
.…(14分)
分析:(Ⅰ)利用求导法则求出f(x)的导函数,令f'(x)=0考虑到判别式大于零得到两个极值点,设x
1<x
2,讨论函数的增减性得到x
1是极大值点,x
2是极小值点,从而利于韦达定理可证;
(Ⅱ) 利用导数法,求函数f(x)在[0,|a|+1]的最大值,从而可得不等式,进而可求a的取值范围.
点评:本题以函数为载体,考查学生求导数及利用导数研究函数极值的能力,灵活运用一元二次方程根与系数的关系解决数学问题的能力. 考查恒成立问题的处理策略,有一定的综合性.

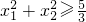 ;
;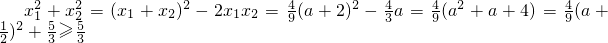 .
.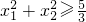 (当且仅当
(当且仅当 时取等号)…(7分)
时取等号)…(7分)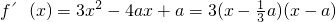 …(8分)
…(8分)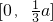 4上增函数,在
4上增函数,在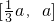 5上为减函数,在[a,a+1]6上为增函数.f(x)在[0,a+1]上的最大值为
5上为减函数,在[a,a+1]6上为增函数.f(x)在[0,a+1]上的最大值为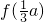 与f(a+1)中的较大者.
与f(a+1)中的较大者. ,f(a+1)=a+1.
,f(a+1)=a+1.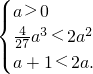 …(9分)
…(9分)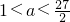 .…(11分)
.…(11分)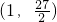 .…(14分)
.…(14分)
