Question

【题目】已知函数.

（1）完成表一中对应的值，并在坐标系中用描点法作出函数的图象：（表一）

	0.25	0.5	0.75	1	1.25	1.5
			0.08		1.82	2.58

（2）根据你所作图象判断函数的单调性，并用定义证明；

（3）说明方程的根在区间存在的理由，并从表二中求使方程的根的近似值达到精确度为0.01时运算次数的最小值并求此时方程的根的近似值，且说明理由.

（表二）二分法的结果

运算次数的值		左端点	右端点
	-0.537	0.6	0.75	0.08
	-0.217	0.675	0.75	0.08
	-0.064	0.7125	0.75	0.08
	-0.064	0.7125	0.73125	0.011
	-0.03	0.721875	0.73125	0.011
	-0.01	0.7265625	0.73125	0.011

Answer 1

【答案】（1）见解析 （2）增函数，证明见解析 （3），方程的根的近似值为，理由见解析

【解析】

(1)分别代入表中的数据进行求解再描点即可.

(2)由图像直观判断即可.再设区间内,判断的正负进行证明即可.

(3)根据零点存在性定理证明即可证明程的根在区间存在.再根据图表判断当根的近似值与的差的绝对值小于时的最小值即可.

解：（1）

		0.5	0.75	1	1.25	1.5
			0.08	1	1.82	2.58

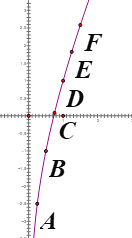
（2）函数在定义域内为增函数,证明：设,则,,因为

即所以函数在定义域内为增函数.

（3）是图象是一条连续不断的曲线,

且,故方程的根在区间存在.

当时,所以当时方程的根的近似值达不到精确度为0.01,

当时,所以当时方程的根的近似值达到精确度为0.01,所以.

方程的根的近似值为.