
分析 Sn+Sn-1=4n2(n≥2,n∈N+),可得S2+S1=16,a1=a,a2=16-2a,Sn+1+Sn=4(n+1)2,可得:an+1+an=8n+4,变形为:an+1-4(n+1)=-(an-4n),对a分类讨论,利用等比数列的通项公式及其已知条件对任意n∈N+,an<an+1恒成立即可得出.
解答 解:∵Sn+Sn-1=4n2(n≥2,n∈N+),∴S2+S1=16,a1=a,可得2a1+a2=16,∴a2=16-2a.
Sn+1+Sn=4(n+1)2,
可得:an+1+an=8n+4,
变形为:an+1-4(n+1)=-(an-4n),
①a≠4时,数列{an-4n}是等比数列,a2-8=8-2a,公比为-1,n≥2.
∴an-4n=(8-2a)×(-1)n-2,
∴an=4n+(8-2a)×(-1)n-2,
∵对任意n∈N+,an<an+1恒成立,∴4n+(8-2a)×(-1)n-2<4(n+1)+(8-2a)×(-1)n-1,化为:1+(4-a)×(-1)n-1>0,
n=2k(k∈N*)时,可得:1-(4-a)>0,解得a>3.
n=2k+1(k∈N*)时,可得:1+(4-a)>0,解得a<5.
∴3<a<5,a≠4.
由a1<a2可得:a<16-2a,解得$a<\frac{16}{3}$,
综上可得:3<a<5,a≠4.
②a=4时,a1=4,a2=8,由an+1-4(n+1)=-(an-4n),可得:an=4n,an+1=4(n+1)
对任意n∈N+,an<an+1恒成立.
综上①②可得:3<a<5.
∴a的取值范围是(3,5).
故答案为:(3,5).
点评 本题考查了递推关系、不等式的解法、等比数列的通项公式,考查了分类讨论方法、推理能力与计算能力,属于难题.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:解答题
| 编号n | 1 | 2 | 3 | 4 | 5 | 6 |
| 成绩xn | 110 | 124 | 130 | x4 | 110 | 111 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10$\sqrt{3}$ | B. | $\frac{10\sqrt{6}}{3}$ | C. | 5$\sqrt{2}$ | D. | 5$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
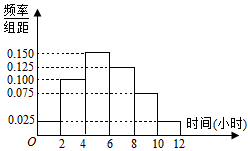 为调查某乡镇中心小学的学生每周平均体育运动时间的情况,收集了20位学生每周平均体育运动时间的样本数据(单位:小时).这20位学生每周平均体育运动时间的频率分布直方图如图所示,其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].
为调查某乡镇中心小学的学生每周平均体育运动时间的情况,收集了20位学生每周平均体育运动时间的样本数据(单位:小时).这20位学生每周平均体育运动时间的频率分布直方图如图所示,其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-4,$\frac{7}{16}$] | B. | [-4,1] | C. | [$\frac{1}{4}$,$\frac{7}{16}$] | D. | [$\frac{1}{4}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com