
【题目】已知函数![]()
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)若![]() 是
是![]() 的极大值点,求
的极大值点,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象是由函数
的图象是由函数![]() 的图象经如下变换得到:先将函数
的图象经如下变换得到:先将函数![]() 图象上所有点的横坐标缩短到原来的
图象上所有点的横坐标缩短到原来的![]() 倍(纵坐标不变),再将所得到的图象向左平移
倍(纵坐标不变),再将所得到的图象向左平移![]() 个单位长度.
个单位长度.
(1)写出函数![]() 的解析式和其图象的对称中心坐标.
的解析式和其图象的对称中心坐标.
(2)已知关于![]() 的方程
的方程![]() 在
在![]() 上有两个不同的解
上有两个不同的解![]() ,
,![]() ,求实数
,求实数![]() 的取值范围和
的取值范围和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,
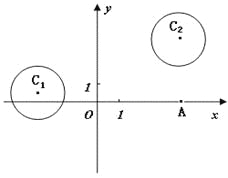
已知圆![]() 和圆
和圆![]() .
.
(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,
,
求直线![]() 的方程;(2)设P为平面上的点,满足:
的方程;(2)设P为平面上的点,满足:
存在过点P的无穷多对互相垂直的直线![]() 和
和![]() ,
,
它们分别与圆![]() 和圆
和圆![]() 相交,且直线
相交,且直线![]() 被圆
被圆![]()
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,试求所有满足条件的点P的坐标。
截得的弦长相等,试求所有满足条件的点P的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
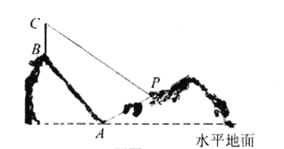
【题目】随着6月6日![]() 商用牌照发放,中国正式进入
商用牌照发放,中国正式进入![]() 商用时代.某人在一山坡
商用时代.某人在一山坡![]() 处观测对面山顶上的一座
处观测对面山顶上的一座![]() 基站(如图),图中所示的山坡均可视为直线,其中基站所在的山坡
基站(如图),图中所示的山坡均可视为直线,其中基站所在的山坡![]() 的坡角为
的坡角为![]() ,点
,点![]() 所在山坡
所在山坡![]() 的坡度为
的坡度为![]() .基站点
.基站点![]() 距坡谷点
距坡谷点![]() 的距离为
的距离为![]() 米,点
米,点![]() 距坡谷点
距坡谷点![]() 的距离为
的距离为![]() 米,且在点
米,且在点![]() 处测得塔顶点
处测得塔顶点![]() 的仰角是
的仰角是![]() .求基站
.求基站![]() 的高度.(参考数据:
的高度.(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,随着中国第一款5G手机投入市场,5G技术已经进入高速发展阶段.已知某5G手机生产厂家通过数据分析,得到如下规律:每生产手机![]() 万台,其总成本为
万台,其总成本为![]() ,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入
,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入![]() 万元满足
万元满足
(1)将利润![]() 表示为产量
表示为产量![]() 万台的函数;
万台的函数;
(2)当产量![]() 为何值时,公司所获利润最大?最大利润为多少万元?
为何值时,公司所获利润最大?最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4cosxsin(x+![]() )-1.
)-1.
(1)求f(x)的最小正周期和单调递减区间;
(2)将y=f(x)图象上所有的点向右平行移动![]() 个单位长度,得到y=g(x)的图象.若g(x)在(0,m)内是单调函数,求实数m的最大值.
个单位长度,得到y=g(x)的图象.若g(x)在(0,m)内是单调函数,求实数m的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com