练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，四棱柱中，平面，，，，，为棱的中点

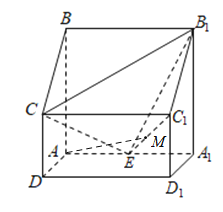
    （1）证明：；

    （2）设点在线段上，且直线与平面所成角的正弦值为，求线段的长.

    【答案】（1）证明见解析；（2）.

    【解析】

    （1）通过勾股定理计算证明证得，再证得，由此证得平面，从而证得.

    （2）建立空间直角坐标系，利用得出点的坐标，根据直线与平面所成角的正弦值为列方程，解方程求得的值，进而求得线段的长.

    （1）在中，，

    ，∴，

    ∵平面，平面∥平面，

    ∴平面，又∥，所以平面，

    所以且

    ∴平面，

    ∴

    （2）由题可知，，，两两垂直，以为原点，分别以，，所在直线为轴，轴，轴建立空间直角坐标系，

    则，，，，，

    ，，设，则

    则

    易知为平面的一个法向量.

    设为直线与平面所成角，则

    解得，（舍去）

    所以，，故线段的长为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某校高三文科名学生参加了月份的高考模拟考试，学校为了了解高三文科学生的历史、地理学习情况，从名学生中抽取名学生的成绩进行统计分析，抽出的名学生的地理、历史成绩如下表：

    地理 历史

    [80,100]

    [60,80）

    [40,60）

    [80,100]

    8

    m

    9

    [60,80）

    9

    n

    9

    [40,60）

    8

    15

    7

    若历史成绩在[80,100]区间的占30%，

    （1）求的值；

    （2）请根据上面抽出的名学生地理、历史成绩，填写下面地理、历史成绩的频数分布表：

    [80,100]

    [60,80）

    [40,60）

    地理

    历史

    根据频数分布表中的数据估计历史和地理的平均成绩及方差（同一组数据用该组区间的中点值作代表），并估计哪个学科成绩更稳定.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C：x2=2py（p＞0）的焦点为F.过F的直线与抛物线C交于A、B，与抛物线C的准线交于M.

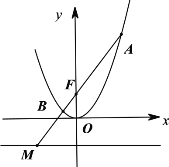
    （1）若|AF|=|FM|=4，求常数p的值；

    （2）设抛物线C在点A、B处的切线相交于N，求动点N的轨迹方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，直三棱柱ABC-A1B1C1中，D,E分别是AB，BB1的中点.

    （Ⅰ）证明： BC1//平面A1CD;

    （Ⅱ）设AA1= AC=CB=2，AB=2，求三棱锥C一A1DE的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    ⑴求函数的单调区间；

    ⑵如果对于任意的，总成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正三棱柱中，（底面为正三角形，侧棱垂直于底面），侧棱长，底面边长，是的中点.

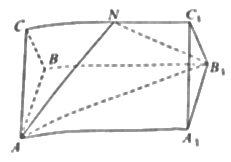
    （1）求证：平面平面；

    （2）设是线段的中点，求直线与平面所成的角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    (1)当时，求的单调区间；

    (2)若是的极大值点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】平面直角坐标系中，直线的参数方程为，（为参数）.以原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）写出直线的极坐标方程与曲线的直角坐标方程；

    （2）已知与直线平行的直线过点，且与曲线交于两点，试求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （Ⅰ）求函数在点点处的切线方程；

    （Ⅱ）当时，恒成立，求的取值范围.

    查看答案和解析>>

    同步练习册答案