
【题目】如图,正三棱柱![]() 中,(底面为正三角形,侧棱垂直于底面),侧棱长
中,(底面为正三角形,侧棱垂直于底面),侧棱长![]() ,底面边长
,底面边长![]() ,
,![]() 是
是![]() 的中点.
的中点.
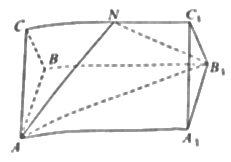
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 是线段
是线段![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x与椭圆E:![]() 1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|
1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|![]() .
.
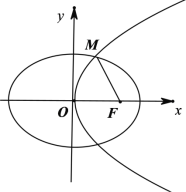
(1)求椭圆E的标准方程;
(2)过点P(1,![]() )的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
)的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过右焦点
,过右焦点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,
两点,![]() 的周长为
的周长为![]() ,点
,点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 、
、![]() 的斜率
的斜率![]() ,
,![]() ,请问
,请问![]() 是否为定值?若是定值,求出其定值;若不是,说明理由.
是否为定值?若是定值,求出其定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
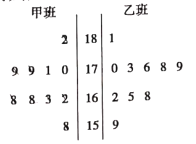
(1)计算甲班的样本方差;
(2)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,
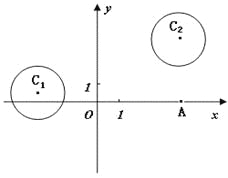
已知圆![]() 和圆
和圆![]() .
.
(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,
,
求直线![]() 的方程;(2)设P为平面上的点,满足:
的方程;(2)设P为平面上的点,满足:
存在过点P的无穷多对互相垂直的直线![]() 和
和![]() ,
,
它们分别与圆![]() 和圆
和圆![]() 相交,且直线
相交,且直线![]() 被圆
被圆![]()
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,试求所有满足条件的点P的坐标。
截得的弦长相等,试求所有满足条件的点P的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为3的正![]() 的各边三等分,过每个分点分别作另外两边的平行线,称
的各边三等分,过每个分点分别作另外两边的平行线,称![]() 的边及这些平行线所交的10个点为格点.若在这10个格点中任取
的边及这些平行线所交的10个点为格点.若在这10个格点中任取![]() 个格点,一定存在三个格点能构成一个等腰三角形(包括正三角形).求
个格点,一定存在三个格点能构成一个等腰三角形(包括正三角形).求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年消毒液和口罩成了抢手年货,老百姓几乎人人都需要,但对于![]() 这种口罩,大多数人不是很了解.现随机抽取40人进行调查,其中45岁以下的有20人,在接受调查的40人中,对于
这种口罩,大多数人不是很了解.现随机抽取40人进行调查,其中45岁以下的有20人,在接受调查的40人中,对于![]() 这种口罩了解的占
这种口罩了解的占![]() ,其中45岁以上(含45岁)的人数占
,其中45岁以上(含45岁)的人数占![]() .
.
(1)将答题卡上的列联表补充完整;
(2)判断是否有![]() 的把握认为对
的把握认为对![]() 这种口罩的了解与否与年龄有关.
这种口罩的了解与否与年龄有关.
参考公式: ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com