
分析 (Ⅰ)根据函数奇偶性的定义判断即可;(Ⅱ)求出g(x)的导数,通过判断导函数的符号,证明出函数的单调性即可;
(Ⅲ)x>0时f(x)>0等价于$\frac{f(x)}{x}>0$,即g(x)>g(1),x<0时f(x)>0等价于$\frac{f(x)}{x}<0$,即g(x)>g(-1),解出即可.
解答 解:(I)因为f(x)(x∈R)是奇函数,
所以$g(-x)=\frac{f(-x)}{-x}=\frac{-f(x)}{-x}=g(x),x≠0$,
所以g(x)是偶函数 …(4分)
(II)因为当x>0时xf'(x)-f(x)<0,
所以$g'(x)=\frac{xf'(x)-f(x)}{x^2}<0$,
所以g(x)在(0,+∞)上为减函数 …(8分)
(III)由(I)f(-1)=0,g(-1)=g(1)=0,…(10分)
x>0时f(x)>0等价于$\frac{f(x)}{x}>0$,即g(x)>g(1),
由(II)所以0<x<1,…(12分)
x<0时f(x)>0等价于$\frac{f(x)}{x}<0$,即g(x)>g(-1),
由(I)( II)g(x)在(-∞,0)上为增函数,
所以x<-1.…(14分)
综上不等式f(x)>0的解集为(-∞,-1)∪(0,1)…(16分)
点评 本题考查了函数的奇偶性、单调性问题,考查导数的应用以及解不等式问题,是一道中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
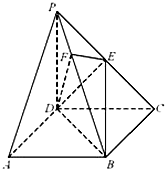 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com