
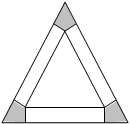
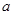 的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为
的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为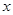 ,容积为
,容积为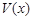 .
.
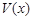 的解析式,并求出函数的定义域;
的解析式,并求出函数的定义域;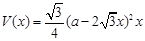 ,定义域为
,定义域为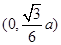 。(Ⅱ)容器高为
。(Ⅱ)容器高为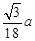 时,容器的容积最大为
时,容器的容积最大为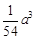 .
.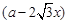 ----2分.
----2分.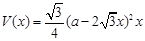 . ---------4分
. ---------4分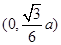 . --------- 5分
. --------- 5分 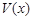 在区间
在区间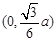 上的最大值点.
上的最大值点.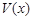 的极值点.
的极值点. 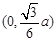 内,
内,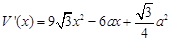 -----------6分
-----------6分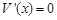 ,即令
,即令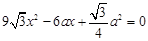 ,解得
,解得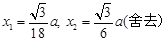 .
.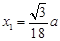 在区间
在区间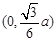 内,
内,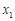 可能是极值点. 当
可能是极值点. 当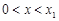 时,
时,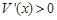 ;
;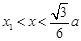 时,
时,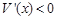 . ------------8分
. ------------8分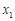 是极大值点,且在区间
是极大值点,且在区间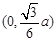 内,
内,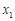 是唯一的极值点,
是唯一的极值点,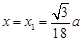 是
是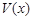 的最大值点,并且最大值
的最大值点,并且最大值 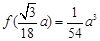
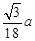 时,容器的容积最大为
时,容器的容积最大为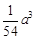 .----------12分
.----------12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com