
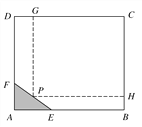
【题目】如图所示,为了保护环境,实现城市绿化,某房地产公司要在拆迁地长方形ABCD处规划一块长方形地面HPGC,建造住宅小区公园,但不能越过文物保护区三角形AEF的边线EF.已知AB=CD=200 m,BC=AD=160 m,AF=40 m,AE=60 m,问如何设计才能使公园占地面积最大,求出最大面积.
【答案】详见解析.
【解析】试题分析: 在EF上取一点P,作PH⊥BC,PG⊥CD,垂足分别为H、G,设PH=x,则140≤x≤200.
由三角形相似得出PG用x表示,进而得出公园占地面积关于x的函数,用配方法得出函数的最值,以及取到最值时的x值.
试题解析:
如题图,在EF上取一点P,作PH⊥BC,PG⊥CD,垂足分别为H、G,设PH=x,则140≤x≤200.
由三角形相似性质PG=120+![]() (200-x),
(200-x),
∴公园占地面积为S=x[120+![]() (200-x)]
(200-x)]
=-![]() x2+
x2+![]() x
x
=-![]() (x-190)2+
(x-190)2+![]() ×1902(140≤x≤200),
×1902(140≤x≤200),
∴当x=190时,Smax=![]() m2.
m2.
答:在EF上取一点P,使P到BC距离为190m时,公园PHCG占地面积最大,最大面积为![]() m2.
m2.
点睛: 本题考查函数的实际应用问题,解决问题的关键是利用相似求出函数的解析式,用二次函数的单调性解决函数的最值.解决函数模型应用的解答题,还有以下几点容易造成失分:①读不懂实际背景,不能将实际问题转化为函数模型.②对涉及的相关公式,记忆错误.③在求解的过程中计算错误.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】通过研究学生的学习行为,专家发现,学生的注意力着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设f(t)表示学生注意力随时间t(分钟)的变化规律\left(f(t)越大,表明学生注意力越集中),经过实验分析得知: 
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,教师能否在学生达到所需的状态下讲授完这道题目?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABCA1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=![]() .
.
(1)求证:C1B⊥平面ABC;
设![]() (0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,
(0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,
试求λ的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,f(x)=2x+![]() (x∈R).
(x∈R).
(1)当x∈(0,1]时,求f(x)的解析式.
(2)判断f(x)在(0,1]上的单调性,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的圆台中,![]() 是下底面圆
是下底面圆![]() 的直径,
的直径,![]() 是上底面圆
是上底面圆![]() 的直径,
的直径,![]() 是圆台的一条母线.
是圆台的一条母线.
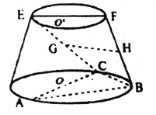
(Ⅰ)已知![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)已知![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值
的余弦值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com