已知f(x)=logax(a>0,且a≠1)
(Ⅰ) 解不等式:f(x+1)-f(1-x)>0;
(Ⅱ) 若f(x)在[2,4]上的最大值比最小值大1,求a的值.
解:(Ⅰ)不等式:f(x+1)-f(1-x)>0 即 即 log
a (x+1)-log
a (-x+1)>0,-
亦即 log
a (x+1)>log
a (-x+1)…1分
(1)当0<a<1时,不等式等价于
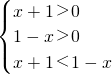
,解得-1<x<0…3分
(2)当a>1时,上述不等式
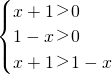
,解得 0<x<1…5分
综上可得,当0<a<1时,不等式的解集为(-1,0); 当a>1时,不等式的解集为(0,1).
(Ⅱ)(1)当0<a<1时,
y=log
a x 在[2,4]上是减函数,故函数的最小值为f(1),最大值为f(2),
由题设得log
a2-log
a4=1,即

=1,∴a=

…7分
(2)当 a>1时,y=log
a x 在[2,4]上是增函数,故函数的最小值为f(2),最大值为f(4),
由题设得 log
a4-log
a2=1,即log
a2=1,∴a=2.
综上得 a=2 或a=

…9分.
分析:(Ⅰ)不等式等价于 log
a (x+1)>log
a (-x+1),分0<a<1和a>1两种情况,分别求得不等式的解集.
(Ⅱ)(1)当0<a<1时,利用函数的单调性可得log
a2-log
a4=1,由此求得a的值.当 a>1时,利用函数的单调性可得 log
a4-log
a2=1,由此求得a的值.综合可得结论.
点评:本题主要考查对数不等式的解法,函数的单调性的应用,体现了分类讨论、以及等价转化的数学思想,属于中档题

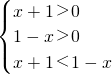 ,解得-1<x<0…3分
,解得-1<x<0…3分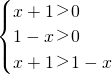 ,解得 0<x<1…5分
,解得 0<x<1…5分 =1,∴a=
=1,∴a= …7分
…7分 …9分.
…9分.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案