
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
分析 求解2a<2b<2,得出a<b<1,loga2<logb2,得出$\left\{\begin{array}{l}{lgb-lga<0}\\{lgalgb>0}\end{array}\right.$或$\left\{\begin{array}{l}{lgb-lga>0}\\{lgalgb<0}\end{array}\right.$,根据对数函数的性质求解即可,再利用充分必要条件的定义判断即可.
解答 解:a、b都是不等于1的正数,
∵2a<2b<2,
∴a<b<1,
∵loga2<logb2,
∴$\frac{1}{lga}<\frac{1}{lgb}$,
即$\frac{lgb-lga}{lgblga}<0$,
∴$\left\{\begin{array}{l}{lgb-lga<0}\\{lgalgb>0}\end{array}\right.$或$\left\{\begin{array}{l}{lgb-lga>0}\\{lgalgb<0}\end{array}\right.$
求解得出:a>b>1或1>a>b>0或b>1,0<a<1
根据充分必要条件定义得出“2a<2b<2”是“loga2>logb2”的充分条不必要件,
故选:B.
点评 本题考查必要条件、充分条件及充分必要条件的判断方法,考查了不等式的性质,是基础题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| 储蓄存款y (千亿元) | 5 | 6 | 7 | 8 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
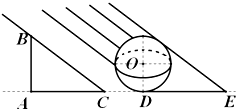 如图,在同一地平面上,有一枝竖直地面的竹杆AB和球O,竹杆的长度和球的直径都是3米,一束太阳光照到竹杆AB留下背影AC长为4米,则该太阳光同时照到球O留下背影DE长为$\frac{9}{2}$米.
如图,在同一地平面上,有一枝竖直地面的竹杆AB和球O,竹杆的长度和球的直径都是3米,一束太阳光照到竹杆AB留下背影AC长为4米,则该太阳光同时照到球O留下背影DE长为$\frac{9}{2}$米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com