
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| 储蓄存款y (千亿元) | 5 | 6 | 7 | 8 | 10 |
分析 (1)由题意,利用公式计算平均数与回归直线的系数,即可写出回归直线方程;
(2)计算t=7时回归方程中$\widehat{y}$的值即可.
解答 解:(1)由题意可知$\overline{t}$=$\frac{1}{5}$×(1+2+3+4+5)=3,
$\overline{y}$=$\frac{1}{5}$×(5+6+7+8+10)=7.2,
$\sum_{i=1}^{n}$tiyi=1×5+2×6+3×7+4×8+5×10=120,
$\sum_{i=1}^{n}$${{t}_{i}}^{2}$=12+22+32+42+52=55,
故$\widehat{b}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$=$\frac{120-5×3×7.2}{55-5{×3}^{2}}$=1.2,
$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{t}$=7.2-1.2×3=3.6,
因此,所求y关于t的回归方程为$\widehat{y}$=3.6+1.2t;
(2)将t=7代入(1)中的回归方程可得:
$\widehat{y}$=3.6+1.2×7=12;
故由所求回归方程可预测该地区2016年的人民币储蓄存款为12千亿元.
点评 本题考查了利用公式计算回归直线的系数,以及回归直线方程的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | y=cos x | B. | y=sin x | C. | y=tan x | D. | y=sin(x-$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
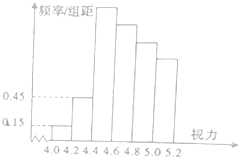 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了若干名学生的体检表,并得到 如直方图:
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了若干名学生的体检表,并得到 如直方图: | 1-50 | 951-1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
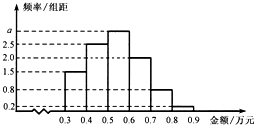 某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.直方图中的a=3.
某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.直方图中的a=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知单位圆O上的两点A,B及单位圆所在平面上的一点P,满足$\overrightarrow{OP}$=m$\overrightarrow{OA}$+$\overrightarrow{OB}$(m为常数).
已知单位圆O上的两点A,B及单位圆所在平面上的一点P,满足$\overrightarrow{OP}$=m$\overrightarrow{OA}$+$\overrightarrow{OB}$(m为常数).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com