
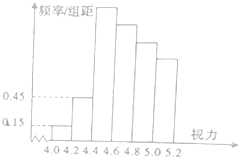
 ijѧУ�о���ѧϰС��Ը�У����ѧ������������е��飬�ڸ�����ȫ��1000��ѧ���������ȡ��������ѧ�������������õ� ��ֱ��ͼ��
ijѧУ�о���ѧϰС��Ը�У����ѧ������������е��飬�ڸ�����ȫ��1000��ѧ���������ȡ��������ѧ�������������õ� ��ֱ��ͼ�� | 1-50 | 951-1000 |
| ���� | 41 | 32 |
| ������ | 9 | 18 |
| P��K2��k�� | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
���� ��I������Ƶ�ʵļ��㷽�����Ȳ�������ȱ����е�ͨ�ʽ�������ʼ��ɵó���
��II������k2�ļ��㹫ʽ�����ݶ����Լ������˼�뼴�ɵó����ۣ�
��� �⣺����������Ƶ��Ϊfi��i=1��2��3��4��5��6����
�����⣬ǰ�����Ƶ�ʳɵȱ����У��������Ƶ�ʳɵȲ����У���f1=0.15��0.2=0.03��f2=0.45��0.2=0.09��${f_3}=\frac{{{f_2}^2}}{f_1}=0.27$��
����$\frac{{��{f_3}+{f_6}��•4}}{2}=1-��0.03+0.09��$���ɵ�f6=0.17��
��������5.0���µ�Ƶ��Ϊ1-0.17=0.83��
��ȫ�꼶������5.0���µ�����ԼΪ1000��0.83=830��
���� ${k^2}=\frac{{100��{{��41��18-32��9��}^2}}}{50��50��73��27}=\frac{300}{73}��4.110��3.841$��
����ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ��
����������9�����꼶������1��50����951��1000���ֱ���3�˺�6�ˣ�X��ȡ0��1��2��3��$P��X=0��=\frac{C_6^3}{C_9^3}=\frac{20}{84}$��$P��X=1��=\frac{C_6^2C_3^1}{C_9^3}=\frac{45}{84}$��$P��X=2��=\frac{C_6^1C_3^2}{C_9^3}=\frac{18}{84}$��$P��X=3��=\frac{C_3^3}{C_9^3}=\frac{1}{84}$��
X�ķֲ���Ϊ��
X����ѧ����$E��X��=0��\frac{20}{84}+1��\frac{45}{84}+2��\frac{18}{84}+3��\frac{1}{84}=1$��
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ�����ʼ���Ӧ�á��ŵ���ʼ��㹫ʽ�������ηֲ��м�����ѧ�����ļ��㹫ʽ�������Լ������˼�룬������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 7 | C�� | 8 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 1 | C�� | $\frac{1}{3}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��� | 2010 | 2011 | 2012 | 2013 | 2014 |
| ʱ�����t | 1 | 2 | 3 | 4 | 5 |
| ������y ��ǧ��Ԫ�� | 5 | 6 | 7 | 8 | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com