练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．①归纳推理是由一般到一般的推理；②归纳推理是由部分到整体的推理；
    ③演绎推理是由一般到特殊的推理；④类比推理是由特殊到特殊的推理；
    ⑤类比推理是由特殊到一般的推理；
    正确的是②③④．

    分析 本题考查的知识点是归纳推理、类比推理和演绎推理的定义，根据定义对5个命题逐一判断即可得到答案．

    解答 解：所谓归纳推理，就是由部分到整体的推理．故①错②对；
    又所谓演绎推理是由一般到特殊的推理．故③对；
    类比推理是由特殊到特殊的推理．故④对⑤错．
    故答案为：②③④

    点评 本题解决的关键是了解归纳推理、演绎推理和类比推理的概念及它们间的区别与联系．判断一个推理过程是否是归纳推理关键是看他是否符合归纳推理的定义，即是否是由特殊到一般的推理过程．判断一个推理过程是否是类比推理关键是看他是否符合类比推理的定义，即是否是由特殊到与它类似的另一个特殊的推理过程．判断一个推理过程是否是演绎推理关键是看他是否符合演绎推理的定义，即是否是由一般到特殊的推理过程．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．已知点F（1，0），圆E：（x+1）2+y2=8，点P是圆E上任意一点，线段PF的垂直平分线和半径PE相交于Q．
    （Ⅰ）求动点Q的轨迹Γ的方程；
    （Ⅱ）若直线l与圆O：x2+y2=1相切，并与（1）中轨迹Γ交于不同的两点A、B，与x轴交于点M，当$\overrightarrow{OA}$•$\overrightarrow{OB}$=λ，且满足$\frac{2}{3}$≤λ≤$\frac{3}{4}$，求$\frac{|AM|}{|BM|}$的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．求出不等式x2-（$\frac{1}{t}$+t）x+1＜0的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．下列函数中，在区间[0，$\frac{π}{2}$]上为减函数的是（　　）
    A．y=cos xB．y=sin xC．y=tan xD．y=sin（x-$\frac{π}{3}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．函数f（x）的导函数f′（x），满足关系式f（x）=x2+3xf′（2）-lnx，则f′（2）的值为（　　）
    A．$\frac{7}{4}$B．-$\frac{7}{4}$C．$\frac{9}{4}$D．-$\frac{9}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．设关于x，y的不等式组$\left\{\begin{array}{l}{2x-y+1＞0}\\{x-m＜0}\\{y+m＞0}\end{array}\right.$表示的平面区域内存在点P（x0，y0）满足x0-2y0=2，则m的取值范围是（　　）
    A．（-∞，3）B．（$\frac{2}{3}$，+∞）C．（2，+∞）D．[$\frac{2}{3}$，2]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．从正方体ABCD A1B1C1D1的8个顶点中选取4个作为四面体的顶点，可得到的不同四面体的个数为（　　）
    A．66B．64C．62D．58

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

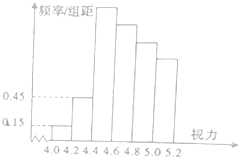    14．某学校研究性学习小组对该校高三学生视力情况进行调查，在高三的全体1000名学生中随机抽取了若干名学生的体检表，并得到 如直方图：
    （Ⅰ）若直方图中前三组的频率成等比数列，后四组的频率成等差数列，试估计全年级视力在5.0以下的人数；
    （Ⅱ）学习小组成员发现，学习成绩突出的学生，近视的比较多，为了研究学生的视力与学习成绩是否有关系，对年纪名次在1～50名和951～1000名的学生进行了调查，得到如图表中数据：
    1-50951-1000
    近视4132
    不近视918
    根据表中的数据，能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系？
    （Ⅲ）在（Ⅱ）中调查的100名学生中，在不近视的学生中按照成绩是否在前50名分层抽样抽取了9人，进一步调查他们良好的护眼习惯，并且在这9人中任取3人，记名次在1～50名的学生人数为X，求X的分布列和数学期望．
    附：
    P（K2≥k）0.100.050.0250.0100.005
    k2.7063.8415.0246.6357.879
    ${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．若集合A，B满足A∩B=B且A≠B，则命题“p：x∈A”是命题“q：x∈B”的必要不充分条件．（填“充分不必要”，“必要不充分”，“充要”）

    查看答案和解析>>

    同步练习册答案