
分析 根据函数f(x)的解析式列出不等式组$\left\{\begin{array}{l}{{2x}^{2}+x-3≥0}\\{3+2x{-x}^{2}>0}\end{array}\right.$,求出解集即可.
解答 解:函数f(x)=$\sqrt{2{x^2}+x-3}$+log3(3+2x-x2),
∴$\left\{\begin{array}{l}{{2x}^{2}+x-3≥0}\\{3+2x{-x}^{2}>0}\end{array}\right.$,
即$\left\{\begin{array}{l}{(2x+3)(x-1)≥0}\\{(x+1)(x-3)<0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x≤-\frac{3}{2}或x≥1}\\{-1<x<3}\end{array}\right.$;
∴函数f(x)的定义域为[1,3).
故答案为:[1,3).
点评 本题考查了根据函数解析式求定义域的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | 66 | B. | 64 | C. | 62 | D. | 58 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
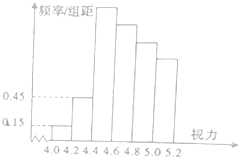 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了若干名学生的体检表,并得到 如直方图:
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了若干名学生的体检表,并得到 如直方图: | 1-50 | 951-1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
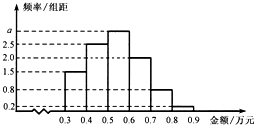 某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.直方图中的a=3.
某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.直方图中的a=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com